19.设x∈R,则“1<x<2”是“|x-2|<1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.阅读如图所示的程序框图,运行相应的程序,则输出i的值为( )
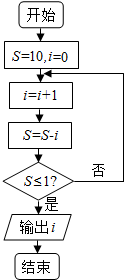

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-2≤0}\\{x-2y≤0}\\{x+2y-8≤0}\end{array}\right.$则目标函数z=3x+y的最大值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 14 |
16.已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则集合A∩∁UB=( )
| A. | {3} | B. | {2,5} | C. | {1,4,6} | D. | {2,3,5} |
14.某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(1)求Z的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
| W | 12 | 15 | 18 |
| P | 0.3 | 0.5 | 0.2 |
(1)求Z的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
12.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如表:
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为($\frac{5π}{12}$,0),求θ的最小值.
0 246374 246382 246388 246392 246398 246400 246404 246410 246412 246418 246424 246428 246430 246434 246440 246442 246448 246452 246454 246458 246460 246464 246466 246468 246469 246470 246472 246473 246474 246476 246478 246482 246484 246488 246490 246494 246500 246502 246508 246512 246514 246518 246524 246530 246532 246538 246542 246544 246550 246554 246560 246568 266669
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(ωx+φ) | 0 | 5 | -5 | 0 |
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为($\frac{5π}{12}$,0),求θ的最小值.
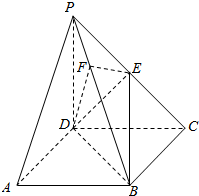 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.