题目内容

17．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-2≤0}\\{x-2y≤0}\\{x+2y-8≤0}\end{array}\right.$则目标函数z=3x+y的最大值为（　　）
A．7B．8C．9D．14

分析 作出不等式组对应的平面区域，利用目标函数的几何意义，求最大值．

解答 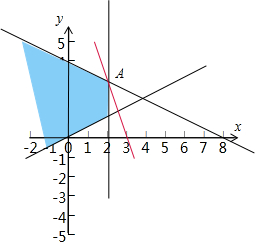解：作出不等式组对应的平面区域如图：（阴影部分）．
由z=3x+y得y=-3x+z，
平移直线y=-3x+z，
由图象可知当直线y=-3x+z经过点A时，直线y=-3x+z的截距最大，
此时z最大．
由$\left\{\begin{array}{l}x-2=0\\ x+2y-8=0\end{array}\right.$，解得$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$，即A（2，3），
代入目标函数z=3x+y得z=3×2+3=9．
即目标函数z=3x+y的最大值为9．
故选：C．

点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．

练习册系列答案
相关题目
7．已知函数f（x）=-2xlnx+x2-2ax+a2，其中a＞0．
（Ⅰ）设g（x）是f（x）的导函数，讨论g（x）的单调性；
（Ⅱ）证明：存在a∈（0，1），使得f（x）≥0恒成立，且f（x）=0在区间（1，+∞）内有唯一解．
8．已知$\overrightarrow{AB}⊥\overrightarrow{AC}，|{\overrightarrow{AB}}|=\frac{1}{t}，|{\overrightarrow{AC}}|=t$，若P点是△ABC所在平面内一点，且$\overrightarrow{AP}=\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|}}+\frac{{4\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|}}$，则$\overrightarrow{PB}•\overrightarrow{PC}$的最大值等于（　　）
A．13B．15C．19D．21
5．设a1，a2，…，an∈R，n≥3．若p：a1，a2，…，an成等比数列；q：（a12+a22+…+an-12）（a22+a32+…+an2）=（a1a2+a2a3+…+an-1an）2，则（　　）
A．p是q的充分条件，但不是q的必要条件
B．p是q的必要条件，但不是q的充分条件
C．p是q的充分必要条件
D．p既不是q的充分条件，也不是q的必要条件
12．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ0$\frac{π}{2}$π$\frac{3π}{2}$2π
x$\frac{π}{3}$$\frac{5π}{6}$
Asin（ωx+φ）05-50
（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（$\frac{5π}{12}$，0），求θ的最小值．
2．已知函数f（x）=$\left\{\begin{array}{l}{2-|x|，x≤2}\\{（x-2）^{2}，x＞2}\end{array}\right.$，函数g（x）=3-f（2-x），则函数y=f（x）-g（x）的零点个数为（　　）
A．2B．3C．4D．5
9．如图，已知AA1⊥平面ABC，BB1∥AA1，AB=AC=3，BC=2$\sqrt{5}$，AA1=$\sqrt{7}$，BB1=2$\sqrt{7}$，点E和F分别为BC和A1C的中点．
（Ⅰ）求证：EF∥平面A1B1BA；
（Ⅱ）求证：平面AEA1⊥平面BCB1；
（Ⅲ）求直线A1B1与平面BCB1所成角的大小．
6．已知数列{an}和{bn}满足a1=2，b1=1，an+1=2an（n∈N*），b1+$\frac{1}{2}$b2+$\frac{1}{3}$b3+…+$\frac{1}{n}$bn=bn+1-1（n∈N*）
（Ⅰ）求an与bn；
（Ⅱ）记数列{anbn}的前n项和为Tn，求Tn．
17．已知某三棱锥的三视图如图所示，则它的外接球体积为$\frac{4}{3}π$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网