Question

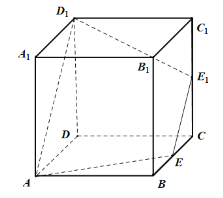
【题目】(2017·衢州调研)已知四棱锥P－ABCD的底面ABCD是菱形，∠ADC＝120°，AD的中点M是顶点P在底面ABCD的射影，N是PC的中点.

(1)求证：平面MPB⊥平面PBC；

(2)若MP＝MC，求直线BN与平面PMC所成角的正弦值.

Answer 1

【答案】(1)见解析（2）

【解析】试题分析:(1)根据菱形性质得MB⊥BC，再根据射影定义得PM⊥平面ABCD ，即得PM⊥BC ，由线面垂直判定定理得BC⊥平面PMB，最后根据面面垂直判定定理得结论，(2)先根据条件建立空间直角坐标系，设立各点坐标，根据方程组解平面PMC法向量，根据向量数量积求向量夹角，最后根据线面角与向量夹角互余关系求直线BN与平面PMC所成角的正弦值.

试题解析: (1)证明　∵四边形ABCD是菱形，∠ADC＝120°，

且M是AD的中点，∴MB⊥AD，∴MB⊥BC.

又∵P在底面ABCD的射影M是AD的中点，

∴PM⊥平面ABCD，

又∵BC平面ABCD，∴PM⊥BC，

而PM∩MB＝M，PM，MB平面PMB，

∴BC⊥平面PMB，又BC平面PBC，

∴平面MPB⊥平面PBC.

(2)解　法一　过点B作BH⊥MC，连接HN，

∵PM⊥平面ABCD，BH平面ABCD，∴BH⊥PM，

又∵PM，MC平面PMC，PM∩MC＝M，

∴BH⊥平面PMC，

∴HN为直线BN在平面PMC上的射影，

∴∠BNH为直线BN与平面PMC所成的角，

在菱形ABCD中，设AB＝2a，则MB＝AB·sin 60°＝a，

MC＝＝a.

又由(1)知MB⊥BC，

∴在△MBC中，BH＝＝a，

由(1)知BC⊥平面PMB，PB平面PMB，

∴PB⊥BC，∴BN＝PC＝a，

∴sin∠BNH＝＝＝.

法二　由(1)知MA，MB，MP两两互相垂直，以M为坐标原点，以MA，MB，MP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系M－xyz，不妨设MA＝1，

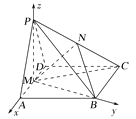
则M(0，0，0)，A(1，0，0)，B(0，，0)，P(0，0，)，C(－2，，0)，

∵N是PC的中点，∴N，

设平面PMC的法向量为n＝(x0，y0，z0)，

又∵＝(0，0，)，＝(－2，，0)，

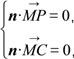∴即

令y0＝1，则n＝，|n|＝，

又∵＝，||＝，

|cos〈，n〉|＝＝.

所以，直线BN与平面PMC所成角的正弦值为.