Question

【题目】设等比数列a1，a2，a3，a4的公比为q，等差数列b1，b2，b3，b4的公差为d，且．记（i1，2，3，4）．

（1）求证：数列不是等差数列；

（2）设， ．若数列是等比数列，求b2关于d的函数关系式及其定义域；

（3）数列能否为等比数列？并说明理由．

Answer 1

【答案】(1)证明见解析；(2)答案见解析；(3)答案见解析.

【解析】试题分析：（1）假设数列是等差数列，则，即，根据 是等差数列及 是等比数列，找出矛盾，假设不成立；（2）由， 得，根据数列是等比数列得，化简求得，再根据，即可求得得范围；（3）方法一：设， ， ， 成等比数列，其公比为，则，解方程组即可；方法二：假设数列是等比数列，则，化简得，即可求得，与且矛盾，故可得证.

试题解析：（1）假设数列是等差数列，则，即．

∵ 是等差数列

∴，从而．

又∵ 是等比数列

∴．

∴，这与矛盾，从而假设不成立．

∴数列不是等差数列．

（2）∵，

∴．

∵

∴，即，

由，得.

∴且．

又∵，

∴，定义域为．

（3）方法一：

设， ， ， 成等比数列，其公比为，则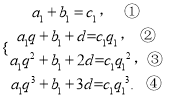

将①+③－2×②得，

将②+④－2×③得，

∵， ，由⑤得， ．

由⑤⑥得，从而．

代入①得．

再代入②，得，与矛盾．

∴， ， ， 不成等比数列．

方法二：

假设数列是等比数列，则．

∴，即．

两边同时减1得， ．

∵等比数列， ， ， 的公比为

∴．

又∵

∴，即．这与且矛盾.

∴假设不成立．

∴数列不能为等比数列．