题目内容
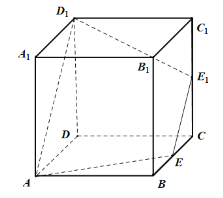
【题目】如图，正方体
的棱长为2，
、
分别为棱
、
上的点，且与顶点不重合.
（1）若直线
与
相交于点
，求证：
、
、三点共线；
（2）若、分别为、的中点.
（ⅰ）求证：几何体
为棱台；
（ⅱ）求棱台的体积.
（附：棱台的体积公式
，其中
、
分别为棱台上下底面积，
为棱台的高）
【答案】（1）证明见解析；（2）（ⅰ）证明见解析；（ⅱ）
【解析】
（1）由
平面
，平面
，平面
平面
，根据点在两个不重合的面内，则点在两个面的公共线上即可证出.
（2）（ⅰ）连
，
、
分别为棱
、
的中点，证出四边形
为梯形，从而可得
与
相交，再由（1）可得直线、
、交于一点，由平面
平面
，即可证出.
（ⅱ）求出
，
，以及棱台的高
，代入棱台的体积公式即可求解.
证明：（1）
，
，
，
平面，
平面，
平面，平面，
即点
为平面与平面的公共点.
又
平面平面，
，即
、
、三点共线.
（2）（ⅰ）连，
、分别为棱、的中点，
为
的中位线，
，
，
，
，
四边形
为平行四边形.
，
，
，
，
四边形为梯形，
与相交.
由（1）知：直线、、交于一点，
又平面平面，
几何体
为三棱台.
（ⅱ）由题意：
，
，，
，
即棱台的体积是.
练习册系列答案
相关题目
