题目内容
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1,F2,短轴的一个端点为P,△PF1F2内切圆的半径为
=1(a>b>0)的两个焦点分别为F1,F2,短轴的一个端点为P,△PF1F2内切圆的半径为![]() ,设过点F2的直线l与被椭圆C截得的线段为RS,当l⊥x轴时,|RS|=3.
,设过点F2的直线l与被椭圆C截得的线段为RS,当l⊥x轴时,|RS|=3.
(1) 求椭圆C的标准方程;
(2) 若点M(0,m),(![]() ),过点M的任一直线与椭圆C相交于两点A.B,y轴上是否存在点N(0,n)使∠ANM=∠BNM恒成立?若存在,判断m、n应满足关系;若不存在,说明理由。
),过点M的任一直线与椭圆C相交于两点A.B,y轴上是否存在点N(0,n)使∠ANM=∠BNM恒成立?若存在,判断m、n应满足关系;若不存在,说明理由。
(3) 在(2)条件下m=1时,求△ABN面积的最大值。
【答案】(1)![]() +
+![]() =1;(2)答案不唯一,见解析;(3)
=1;(2)答案不唯一,见解析;(3)![]() .
.
【解析】
(1)由内切圆半径表示三角形的面积,可得![]() ,再由
,再由![]() ,求得椭圆方程;
,求得椭圆方程;
(2)分![]() 轴和
轴和![]() 不垂直于
不垂直于![]() 轴时两种情况,当AB与x轴不垂直时,设直线AB的方程为y=kx+m,直线与椭圆方程联立,
轴时两种情况,当AB与x轴不垂直时,设直线AB的方程为y=kx+m,直线与椭圆方程联立,![]() ,代入根与系数的关系,得到
,代入根与系数的关系,得到![]() 的关系;
的关系;
(3)由(2)得n=3 M(0,1).N(0,3)设直线AB的方程为y=kx+1,也椭圆方程联立,得到根与系数的关系,并表示面积![]() ,代入根与系数的关系,利用基本不等式求最值.
,代入根与系数的关系,利用基本不等式求最值.
(1)由内切圆的性质,得![]() ×2c×b=
×2c×b=![]() ×(2a+2c)×
×(2a+2c)×![]() ,得
,得![]() =
=![]() .
.
将x=c代入![]() +
+![]() =1,得y=±
=1,得y=±![]() ,所以
,所以![]() =3.
=3.
又a2=b2+c2,所以a=2,b=![]() ,故椭圆C的标准方程为
,故椭圆C的标准方程为![]() +
+![]() =1.
=1.
(2) ①当AB⊥x轴时,可知∠ANM=∠BNM=0.
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.
联立方程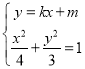 消去y得,(3+4k2)x2+8kmx+4m2-12=0.(
消去y得,(3+4k2)x2+8kmx+4m2-12=0.(![]() )
)
设A(x1,y1),B(x2,y2),则![]() ,x1x2=
,x1x2=![]() .
.
假设存在N(0,n)
则kAN+kBN=![]()
=
![]() =0.(*),对任意k∈R恒成立.
=0.(*),对任意k∈R恒成立.
所以mn=3且m≠0.
m=0时由(*)式知不存在点N符合题意,
综上:m=0时不存在,![]() 时存在点N(0,n),mn=3。
时存在点N(0,n),mn=3。
(3)由(2)得n=3 M(0,1).N(0,3)设直线AB的方程为y=kx+1.
由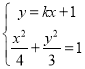
![]()
设A(x1,y1),B(x2,y2),则![]() ,x1x2=
,x1x2=![]() .
.
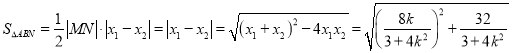
 ,令
,令![]() 则t ≥1,
则t ≥1,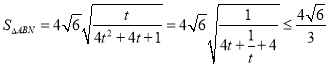
当且仅当 t=1,k=0时 取的最大值。
所以△ABN面积的最大值为![]()

 名校课堂系列答案
名校课堂系列答案【题目】“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入![]() (单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
(单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
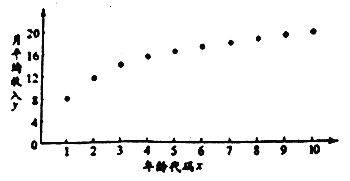
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
附注:①参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为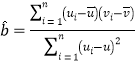 ,
,![]() .
.
③新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税 级数 | 每月应纳税所得额(含税) | 税率 | 每月应纳税所得额(含税) | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|
【题目】如表是某位同学连续5次周考的数学、物理的成绩,结果如下:
周次 | 1 | 2 | 3 | 4 | 5 |
数学( | 79 | 81 | 83 | 85 | 87 |
物理( | 77 | 79 | 79 | 82 | 83 |
参考公式: ,
,![]() ,
,![]() 表示样本均值.
表示样本均值.
(1)求该生5次月考数学成绩的平均分和物理成绩的方差;
(2)一般来说,学生的数学成绩与物理成绩有较强的线性相关关系,根据上表提供的数据,求两个变量![]() 的线性回归方程.
的线性回归方程.
