题目内容
【题目】已知数列
、
满足
，其中
数列的前
项和，
（1）若数列是首项为
.公比为
的等比数列，求数列的通项公式；
（2）若
，
求证：数列满足
，并写出的通项公式；
（3）在（2）的条件下，设
，求证
中任意一项总可以表示成该数列其它两项之积.
【答案】（1）
；（2）等差，
；（3）见解析.
【解析】
（1）数列
是首项为
.公比为
的等比数列求出
，然后求解数列
的通项公式。（2）
，通过
，求出。（3）由（2）可求得
，对于给定的
，若存在
，
，且
，使得
，证明
，然后证明数列
中的任意一项总可以表示成该数列其他两项之积
（1）
数列是首项为.公比为的等比数列
，
。
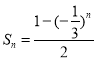所以
（2）若，
所以
所以
即
所以
所以
又
所以数列是首项是2，公差为1的等差数列
所以
（3）证明：由（2）知
对于给定的，若存在
，且，使得
只需
只需
取
，则
所以对于任意数列中任意一项
都存在
和
使得
即中任意一项总可以表示成该数列其它两项之积.
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某工厂有两个车间生产同一种产品，第一车间有工人200人，第二车间有工人400人，为比较两个车间工人的生产效率，采用分层抽样的方法抽取工人，并对他们中每位工人生产完成一件产品的时间（单位：min）分别进行统计，得到下列统计图表（按照[55，65），[65，75），[75，85），[85，95]分组）．
分组 | 频数 |
[55，65） | 2 |
[65，75） | 4 |
[75，85） | 10 |
[85，95] | 4 |
合计 | 20 |
第一车间样本频数分布表
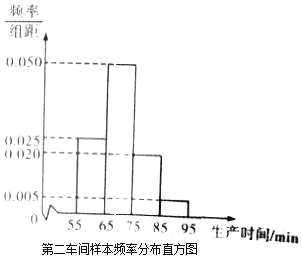
（Ⅰ）分别估计两个车间工人中，生产一件产品时间小于75min的人数；
（Ⅱ）分别估计两车间工人生产时间的平均值，并推测哪个车间工人的生产效率更高？（同一组中的数据以这组数据所在区间中点的值作代表）
（Ⅲ）从第一车间被统计的生产时间小于75min的工人中随机抽取2人，求抽取的2人中，至少1人生产时间小于65min的概率．
