题目内容
设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4…).
(1)求证: 数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(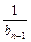 )(n=2,3,4…),求数列{bn}的通项bn;
)(n=2,3,4…),求数列{bn}的通项bn;
(3)求和: b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1.
(1)求证: 数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(
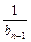 )(n=2,3,4…),求数列{bn}的通项bn;
)(n=2,3,4…),求数列{bn}的通项bn;(3)求和: b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1.
(1)证明略 (2) bn=1+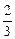 (n-1)=
(n-1)=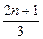 (3) b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1-
(3) b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1-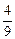 (2n2+3n)
(2n2+3n)
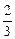 (n-1)=
(n-1)=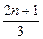 (3) b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1-
(3) b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1-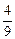 (2n2+3n)
(2n2+3n)(1)由S1=a1=1,S2=1+a2,得3t(1+a2)-(2t+3)=3t.
∴a2=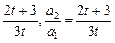 .
.
又3tSn-(2t+3)Sn-1=3t, ①
3tSn-1-(2t+3)Sn-2=3t ②
①-②得3tan-(2t+3)an-1=0
∴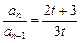 ,n=2,3,4…,
,n=2,3,4…,
所以{an}是一个首项为1公比为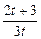 的等比数列;
的等比数列;
(2)由f(t)=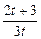 =
=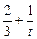 ,得bn=f(
,得bn=f(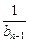 )=
)=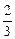 +bn-1.
+bn-1.
可见{bn}是一个首项为1,公差为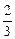 的等差数列.
的等差数列.
于是bn=1+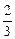 (n-1)=
(n-1)=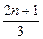 ;
;
(3)由bn=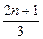 ,可知
,可知
{b2n-1}和{b2n}是首项分别为1和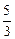 ,公差均为
,公差均为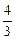 的等差数列,
的等差数列,
于是b2n=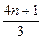 ,
,
∴b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=-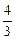 (b2+b4+…+b2n)=-
(b2+b4+…+b2n)=-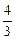 ·
·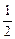 n(
n(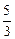 +
+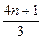 )=-
)=-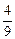 (2n2+3n).
(2n2+3n).
∴a2=
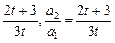 .
.又3tSn-(2t+3)Sn-1=3t, ①
3tSn-1-(2t+3)Sn-2=3t ②
①-②得3tan-(2t+3)an-1=0

∴
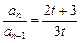 ,n=2,3,4…,
,n=2,3,4…,所以{an}是一个首项为1公比为
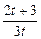 的等比数列;
的等比数列;(2)由f(t)=
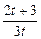 =
=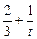 ,得bn=f(
,得bn=f(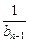 )=
)=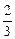 +bn-1.
+bn-1.可见{bn}是一个首项为1,公差为
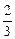 的等差数列.
的等差数列.于是bn=1+
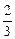 (n-1)=
(n-1)=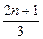 ;
;(3)由bn=
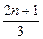 ,可知
,可知{b2n-1}和{b2n}是首项分别为1和
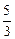 ,公差均为
,公差均为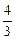 的等差数列,
的等差数列,于是b2n=
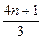 ,
,∴b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=-
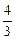 (b2+b4+…+b2n)=-
(b2+b4+…+b2n)=-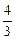 ·
·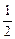 n(
n(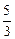 +
+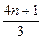 )=-
)=-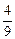 (2n2+3n).
(2n2+3n).
练习册系列答案
相关题目
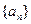 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列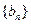 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,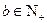 ,且
,且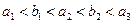 .
.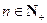 ,总存在
,总存在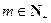 ,使
,使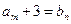 ,求b的值;
,求b的值;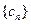 是所有
是所有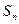 为
为
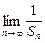 ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;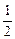 ,求数列{
,求数列{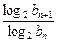 }的最大项和最小项的值.
}的最大项和最小项的值. 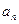 }的前n项和为
}的前n项和为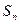 ,若
,若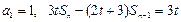 (t为正常数,n=2,3,4…).
(t为正常数,n=2,3,4…).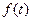 ,作数列
,作数列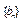 使
使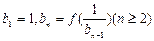 ,试求
,试求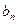 ,并求
,并求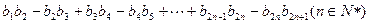
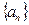 中,
中,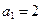 ,n≥2时
,n≥2时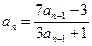 ,求通项公式.
,求通项公式.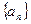 及等比数列
及等比数列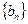 中,
中,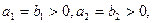 则当
则当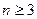 时有
时有



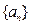 中,
中,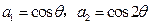 ,且
,且 .求
.求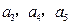 ,由此推出
,由此推出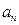 表达式.
表达式.