题目内容
等差数列{an}的前n项的和为30,前2m项的和为100,求它的前3m项的和为_________.
210
解法一: 将Sm=30,S2m=100代入Sn=na1+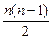 d,得:
d,得:
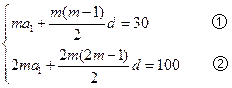
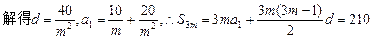
解法二:由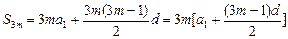 知,
知,
要求S3m只需求m[a1+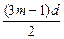 ],
],
将②-①得ma1+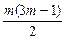 d=70,∴S3m=210.
d=70,∴S3m=210.
解法三:由等差数列{an}的前n项和公式知,Sn是关于n的二次函数,即Sn=An2+Bn(A、B是常数).
将Sm=30,S2m=100代入,得
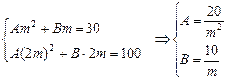 ,∴S3m=A·(3m)2+B·3m=210
,∴S3m=A·(3m)2+B·3m=210
解法四:
S3m=S2m+a2m+1+a2m+2+…+a3m
=S2m+(a1+2md)+…+(am+2md)
=S2m+(a1+…+am)+m·2md
=S2m+Sm+2m2d
由解法一知d=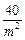 ,代入得S3m=210
,代入得S3m=210
解法五:根据等差数列性质知 Sm,S2m-Sm,S3m-S2m也成等差数列,
Sm,S2m-Sm,S3m-S2m也成等差数列,
从而有: 2(S2m-Sm)=Sm+(S3m-S2m)
∴S3m=3(S2m-Sm)=210
解法六:∵Sn=na1+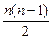 d,
d,
∴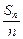 =a1+
=a1+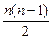 d
d
∴点(n,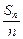 )是直线y=
)是直线y=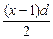 +a1上的一串点,
+a1上的一串点,
由三点(m,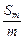 ),(2m,
),(2m,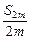 ),(3m,
),(3m,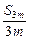 )共线,易得S3m=3(S2m-Sm)=210
)共线,易得S3m=3(S2m-Sm)=210
解法七: 令m=1得S1=30,S2=100,得a1=30,a1+a2=100,∴a1=30,a2=70
∴a3=70+(70-30)=110
∴S3=a1+a2+a3=210
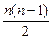 d,得:
d,得: 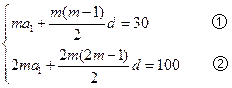
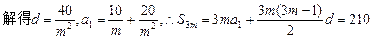
解法二:由
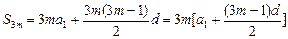 知,
知,要求S3m只需求m[a1+
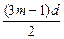 ],
],将②-①得ma1+
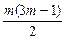 d=70,∴S3m=210.
d=70,∴S3m=210.解法三:由等差数列{an}的前n项和公式知,Sn是关于n的二次函数,即Sn=An2+Bn(A、B是常数).
将Sm=30,S2m=100代入,得
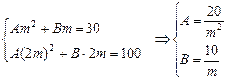 ,∴S3m=A·(3m)2+B·3m=210
,∴S3m=A·(3m)2+B·3m=210解法四:
S3m=S2m+a2m+1+a2m+2+…+a3m
=S2m+(a1+2md)+…+(am+2md)
=S2m+(a1+…+am)+m·2md
=S2m+Sm+2m2d

由解法一知d=
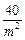 ,代入得S3m=210
,代入得S3m=210
解法五:根据等差数列性质知
 Sm,S2m-Sm,S3m-S2m也成等差数列,
Sm,S2m-Sm,S3m-S2m也成等差数列,从而有: 2(S2m-Sm)=Sm+(S3m-S2m)
∴S3m=3(S2m-Sm)=210
解法六:∵Sn=na1+
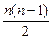 d,
d,∴
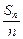 =a1+
=a1+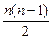 d
d∴点(n,
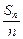 )是直线y=
)是直线y=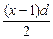 +a1上的一串点,
+a1上的一串点,由三点(m,
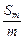 ),(2m,
),(2m,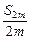 ),(3m,
),(3m,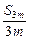 )共线,易得S3m=3(S2m-Sm)=210
)共线,易得S3m=3(S2m-Sm)=210
解法七: 令m=1得S1=30,S2=100,得a1=30,a1+a2=100,∴a1=30,a2=70
∴a3=70+(70-30)=110
∴S3=a1+a2+a3=210

练习册系列答案
相关题目
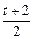 处取得最小值-
处取得最小值-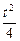 (t>0),f(1)=0.
(t>0),f(1)=0.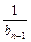 )(n=2,3,4…),求数列{bn}的通项bn;
)(n=2,3,4…),求数列{bn}的通项bn;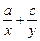 =_________
=_________
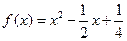 ,
,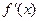 为函数
为函数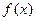 的导函数.
的导函数.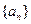 满足:
满足: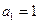 ,
,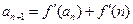 (
(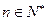 ),求数列
),求数列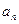 ;
;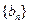 满足:
满足: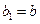 ,
,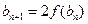 (
(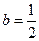 时,数列
时,数列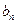 ;若不是,请说明理由;
;若不是,请说明理由;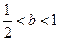 时, 求证:
时, 求证: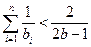 .
. 中,
中,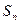 是其前
是其前 项和,
项和,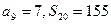 ,求:
,求: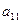 及
及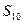 .
.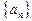 中
中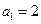 ,点
,点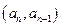 在函数
在函数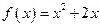 的图
的图 像上
像上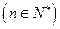 ,(1)求
,(1)求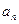 ,(2)若
,(2)若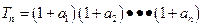 ,求
,求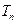 .
.