题目内容
设数列{
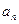 }的前n项和为
}的前n项和为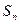 ,若
,若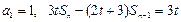 (t为正常数,n=2,3,4…).
(t为正常数,n=2,3,4…).(1)求证:{
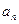 }为等比数列;(2)设{
}为等比数列;(2)设{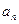 }公比为
}公比为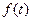 ,作数列
,作数列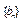 使
使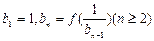 ,试求
,试求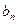 ,并求
,并求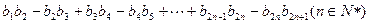
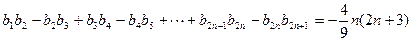 ,
,(1)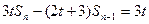
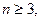
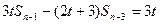 ,相减得
,相减得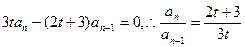 (常数)
(常数)
又当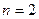 ,
,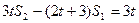
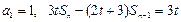 ,
,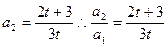 ,
,
故{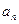 }为等比数列;
}为等比数列;
(2)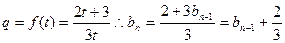 ,故{
,故{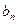 }为等差数列,
}为等差数列,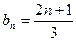 ,
,
所以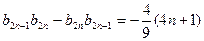 ,
,
故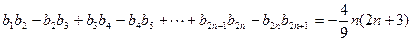 .
.
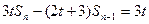
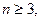
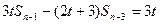 ,相减得
,相减得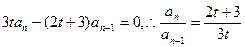 (常数)
(常数)又当
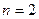 ,
,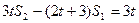
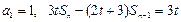 ,
,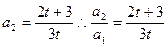 ,
,故{
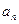 }为等比数列;
}为等比数列;(2)
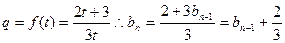 ,故{
,故{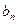 }为等差数列,
}为等差数列,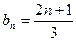 ,
,所以
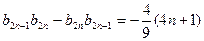 ,
,故
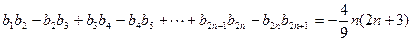 .
.
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
题目内容
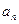 }的前n项和为
}的前n项和为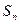 ,若
,若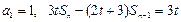 (t为正常数,n=2,3,4…).
(t为正常数,n=2,3,4…).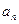 }为等比数列;(2)设{
}为等比数列;(2)设{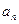 }公比为
}公比为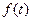 ,作数列
,作数列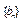 使
使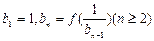 ,试求
,试求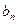 ,并求
,并求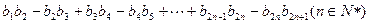
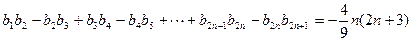 ,
,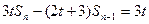
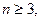
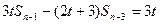 ,相减得
,相减得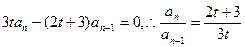 (常数)
(常数)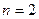 ,
,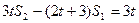
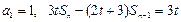 ,
,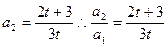 ,
,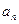 }为等比数列;
}为等比数列;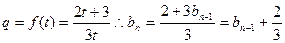 ,故{
,故{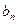 }为等差数列,
}为等差数列,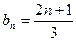 ,
,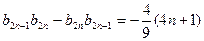 ,
,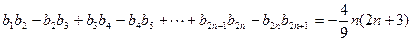 .
.
 小题狂做系列答案
小题狂做系列答案