��Ŀ����
1��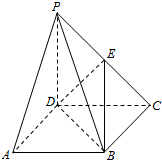 �������������У�������Ϊ����������һ����������洹ֱ��������֮Ϊ���������ĸ��涼Ϊֱ�������ε��������֮Ϊ��Ğ������ͼ��ʾ������P-ABCD�У�����PD�͵���ABCD����PD=CD����E��PC���е㣬����DE��BD��BE��
�������������У�������Ϊ����������һ����������洹ֱ��������֮Ϊ���������ĸ��涼Ϊֱ�������ε��������֮Ϊ��Ğ������ͼ��ʾ������P-ABCD�У�����PD�͵���ABCD����PD=CD����E��PC���е㣬����DE��BD��BE������֤����DE��ƽ��PBC�����ж�������EBCD�Ƿ�Ϊ��Ğ�����ǣ�д����ÿ�����ֱ�ǣ�ֻ��д�����ۣ��������ǣ���˵�����ɣ�
��������P-ABCD�����ΪV1��������EBCD�����ΪV2����$\frac{V_1}{V_2}$��ֵ��
���� ����֤��BC��ƽ��PCD��DE��ƽ��PBC����֪������EBCD���ĸ��涼��ֱ�������Σ����ɵó����ۣ�
��������֪��PD������P-ABCD�ĸߣ�����V1=$\frac{1}{3}{S}_{ABCD}•PD$=$\frac{1}{3}BC•CD•PD$���ɣ���֪��DE�DZ�ĞD-BCE�ĸߣ�BC��CE������V2=$\frac{1}{3}{S}_{��BCE}•DE$=$\frac{1}{6}BC•CE•DE$��������$\frac{V_1}{V_2}$��ֵ��
��� ����֤������ΪPD�͵���ABCD������PD��BC��
��ΪABCDΪ�����Σ�����BC��CD��
��ΪPD��CD=D��
����BC��ƽ��PCD��
��ΪDE?ƽ��PCD��
����BC��DE��
��ΪPD=CD����E��PC���е㣬
����DE��PC��
��ΪPC��BC=C��
����DE��ƽ��PBC��
��BC��ƽ��PCD��DE��ƽ��PBC����֪������EBCD���ĸ��涼��ֱ�������Σ�
��������EBCD��һ����Ğ�����ĸ����ֱ�Ƿֱ��ǡ�BCD����BCE����DEC����DEB��
��������֪��PD������P-ABCD�ĸߣ�����V1=$\frac{1}{3}{S}_{ABCD}•PD$=$\frac{1}{3}BC•CD•PD$��
�ɣ���֪��DE�DZ�ĞD-BCE�ĸߣ�BC��CE��
����V2=$\frac{1}{3}{S}_{��BCE}•DE$=$\frac{1}{6}BC•CE•DE$��
��ΪPD=CD����E��PC���е㣬
����DE=CE=$\frac{\sqrt{2}}{2}$CD��
����$\frac{{V}_{1}}{{V}_{2}}$=$\frac{\frac{1}{3}BC•CD•PD}{\frac{1}{6}BC•CE•DE}$=$\frac{2CD•PD}{CE•DE}$=4
���� ���⿼�����洹ֱ���ж������ʣ���������ļ��㣬����ѧ�������������������������е��⣮

| A�� | -1 | B�� | -2 | C�� | -5 | D�� | 1 |
| A�� | $\frac{3}{4}$+$\frac{1}{2��}$ | B�� | $\frac{1}{2}$+$\frac{1}{��}$ | C�� | $\frac{1}{2}$-$\frac{1}{��}$ | D�� | $\frac{1}{4}$-$\frac{1}{2��}$ |
| A�� | x��y����أ�x��z����� | B�� | x��y����أ�x��z����� | ||
| C�� | x��y����أ�x��z����� | D�� | x��y����أ�x��z����� |
| A�� | ��-1��3�� | B�� | ��-1��0�� | C�� | ��0��2�� | D�� | ��2��3�� |