题目内容
10.在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°.动点E和F分别在线段BC和DC上,且$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,$\overrightarrow{DF}$=$\frac{1}{9λ}\overrightarrow{DC}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值为$\frac{29}{18}$.分析 利用等腰梯形的性质结合向量的数量积公式将所求表示为关于λ的代数式,根据具体的形式求最值.
解答 解:由题意,得到AD=BC=CD=1,所以$\overrightarrow{AE}$•$\overrightarrow{AF}$=($\overrightarrow{AB}+\overrightarrow{BE}$)•($\overrightarrow{AD}+\overrightarrow{DF}$)=($\overrightarrow{AB}+λ\overrightarrow{BC}$)•($\overrightarrow{AD}+\frac{1}{9λ}\overrightarrow{DC}$)
=$\overrightarrow{AB}•\overrightarrow{AD}+λ\overrightarrow{BC}•\overrightarrow{AD}+\frac{1}{9λ}\overrightarrow{AB}•\overrightarrow{DC}$$+\frac{1}{9}\overrightarrow{BC}•\overrightarrow{DC}$=2×1×cos60°+λ1×1×cos60°+$\frac{1}{9λ}$×2×1+$\frac{1}{9}$×1×1×cos120°
=1+$\frac{λ}{2}$+$\frac{2}{9λ}$-$\frac{1}{18}$≥$\frac{17}{18}$+$\frac{2}{3}$=$\frac{29}{18}$(当且仅当$\frac{λ}{2}=\frac{2}{9λ}$时等号成立);
故答案为:$\frac{29}{18}$.
点评 本题考查了等腰梯形的性质以及向量的数量积公式的运用、基本不等式求最值;关键是正确表示所求,利用基本不等式求最小值.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 |
| 1 2 3 4 5 6 7 8 9 | 40 44 40 41 33 40 45 42 43 | 10 11 12 13 14 15 16 17 18 | 36 31 38 39 43 45 39 38 36 | 19 20 21 22 23 24 25 26 27 | 27 43 41 37 34 42 37 44 42 | 28 29 30 31 32 33 34 35 36 | 34 39 43 38 42 53 37 49 39 |
(2)计算(1)中样本的均值$\overline{x}$和方差s2;
(3)36名工人中年龄在$\overline{x}$-s和$\overline{x}$+s之间有多少人?所占百分比是多少(精确到0.01%)?
| A. | $\frac{{x}^{2}}{21}$-$\frac{{y}^{2}}{28}$=1 | B. | $\frac{{x}^{2}}{28}$-$\frac{{y}^{2}}{21}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
| A. | [0,1) | B. | (0,2] | C. | (1,2) | D. | [1,2] |
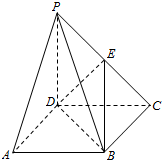 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE、BD、BE.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE、BD、BE.