题目内容
13.已知双曲线过点$(4,\sqrt{3})$且渐近线方程为y=±$\frac{1}{2}$x,则该双曲线的标准方程是$\frac{1}{4}$x2-y2=1.分析 设双曲线方程为y2-$\frac{1}{4}$x2=λ,代入点$(4,\sqrt{3})$,求出λ,即可求出双曲线的标准方程.
解答 解:设双曲线方程为y2-$\frac{1}{4}$x2=λ,
代入点$(4,\sqrt{3})$,可得3-$\frac{1}{4}×16$=λ,
∴λ=-1,
∴双曲线的标准方程是$\frac{1}{4}$x2-y2=1.
故答案为:$\frac{1}{4}$x2-y2=1.
点评 本题考查双曲线的标准方程,考查学生的计算能力,正确设出双曲线的方程是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知点A(0,1),B(3,2),向量$\overrightarrow{AC}$=(-4,-3),则向量$\overrightarrow{BC}$=( )
| A. | (-7,-4) | B. | (7,4) | C. | (-1,4) | D. | (1,4) |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1 (a>0,b>0)的一条渐近线过点(2,$\sqrt{3}$),且双曲线的一个焦点在抛物线y2=4$\sqrt{7}$x的准线上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{21}$-$\frac{{y}^{2}}{28}$=1 | B. | $\frac{{x}^{2}}{28}$-$\frac{{y}^{2}}{21}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
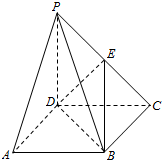 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE、BD、BE.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE、BD、BE. 如图,在△ABC中,AB=AC,△ABC的外接圆⊙O的弦AE交BC于点D.
如图,在△ABC中,AB=AC,△ABC的外接圆⊙O的弦AE交BC于点D.