Question

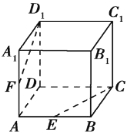
【题目】如图所示的平面图形中，ABCD是边长为2的正方形，△HDA和△GDC都是以D为直角顶点的等腰直角三角形，点E是线段GC的中点．现将△HDA和△GDC分别沿着DA，DC翻折，直到点H和G重合为点P．连接PB，得如图的四棱锥．

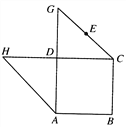
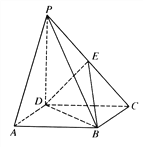
（Ⅰ）求证：PA//平面EBD；

（Ⅱ）求二面角大小．

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）60o.

【解析】试题分析：（1）连接AC交BD于点O，连接EO，由EO为△CPA的中位线，能证明PA//平面EDB （2）分别求出平面PBD和PBC的法向量，利用向量法能求出二面角的大小

试题解析：

（Ⅰ）证明：连接AC交BD于点O，

连接EO，因为四边形ABCD

是正方形，所以O为AC的中点，

又因为E为PC中点，

所以EO为△CPA的中位线，

所以EO//PA

因为EO平面EDB，PA平面EDB

所以PA//平面EDB

（Ⅱ）由题意有，

故DA，DC，DP两两垂直

如图，以D为原点建立空间直角坐标系

有

由题知

又因为AC平面ABCD，所以，

又，，所以

所以平面PBD的法向量是

设平面PBC的法向量，

由于，

则有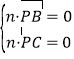，所以

令，得

则

由图可知求二面角的平面角为锐角，

所以二面角的大小为60o