题目内容
【题目】在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布
N(-1,1)的部分密度曲线)的点的个数的估计值为
附:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.682 6,P(μ-2σ<X<μ+2σ)=0.954 4.
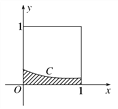
A. 1 193 B. 1 359 C. 2 718 D. 3 413
【答案】B
【解析】正态分布的图象如下图:
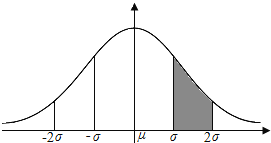
正态分布N(﹣1,1)则在(0,1)的概率如上图阴影部分,
其概率为![]() ×[P(μ﹣2σ<X≤μ+2σ)﹣P(μ﹣σ<X≤μ+σ)]=
×[P(μ﹣2σ<X≤μ+2σ)﹣P(μ﹣σ<X≤μ+σ)]= ![]() ×(0.9544﹣0.6826)=0.1359;
×(0.9544﹣0.6826)=0.1359;
即阴影部分的面积为0.1359;
所以点落入图中阴影部分的概率为p= ![]() =0.1359;
=0.1359;
投入10000个点,落入阴影部分的个数期望为10000×0.1359=1359.
故选B.

练习册系列答案
相关题目
【题目】某校高三一次月考之后,为了为解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成了下面频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 5 | 0.05 |
第二组 |
| 35 | 0.35 |
第三组 |
| 30 | 0.30 |
第四组 |
| 20 | 0.20 |
第五组 |
| 10 | 0.10 |
合计 | 100 | 1.00 | |
(1)试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在![]() 中的学生数为
中的学生数为![]() ,
,
求:①在三次抽取过程中至少有两次连续抽中成绩在![]() 中的概率;
中的概率;
②![]() 的分布列和数学期望.(注:本小题结果用分数表示)
的分布列和数学期望.(注:本小题结果用分数表示)