题目内容
【题目】西北某省会城市计划新修一座城市运动公园，设计平面如图所示：其为五边形
，其中三角形区域
为球类活动场所；四边形
为文艺活动场所，
，为运动小道（不考虑宽度）
，
，
千米.
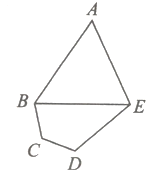
（1）求小道
的长度；
（2）求球类活动场所
的面积最大值.
【答案】（1）
（2）
【解析】
（1）连接BD，在△BCD中由余弦定理得BD的值，在Rt△BDE中，求解BE即可；
（2）设∠ABE＝α，在△ABE中，由正弦定理求解AB，AE，表示S△ABE，然后求解最大值．
如解图所示，连接
，
（1）在三角形
中，
千米，
，
由余弦定理得：
，
所以
∵
，，∴
∵
，∴
在
中，
（千米）
∴小道
的长度为千米；
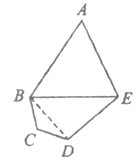
（2）如图所示，设
，∵
，
∴
在三角形
中，由正弦定理可得：
，
∴
，
，
∴
，
，
，
∵
，∴
，
故当
时，
取得最大值，最大值为
.
∴球类活动场所
的面积最大值为平方千米.
练习册系列答案
相关题目
【题目】某海滨浴场一天的海浪高度
是时间
的函数，记作
，下表是某天各时的浪高数据：
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
（1）选用一个三角函数来近似描述这个海滨浴场的海浪高度与时间
的函数关系；
（2）依据规定，当海浪高度不少于
时才对冲浪爱好者开放海滨浴场，请依据（1）的结论，判断一天内的
至
之间，有多少时间可供冲浪爱好者进行冲浪？
