Question

【题目】已知双曲线的离心率为2，过点、斜率为1的直线与双曲线交于、两点且，.

（1）求双曲线方程。

（2）设为双曲线右支上动点，为双曲线的右焦点，在轴负半轴上是否存在定点，使得？若存在，求出点的坐标；若不存在，请说明理由。

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）由双曲线离心率为2知，.

于是，双曲线方程可化为.

又直线，与双曲线方程联立得

①

设点，.则

，. ②

因为，所以，

.故.

结合，解得，.

代入式②得

又

，

从而，.

此时，，代入式①并整理得

.

显然，该方程有两个不同的实根.

因此，符合要求.故双曲线的方程为

（2）假设点存在.由（1）知双曲线右焦点为.

设为双曲线右支上一点.

当时，，.

因为，所以，.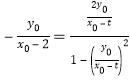

将代入上式并整理得

.

当时，，而时，，符合.

所以，满足条件的点存在.