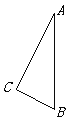
题目内容
【题目】在极坐标系中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 与
与![]() ,
,![]() 交于不同四点,这四点在
交于不同四点,这四点在![]() 上的排列顺次为
上的排列顺次为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:(1)极坐标方程化为直角坐标方程可得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .曲线
.曲线![]() 的直角坐标方程为:
的直角坐标方程为: ![]() .
.
(2)不妨设四个交点自下而上依次为![]() ,它们对应的参数分别为
,它们对应的参数分别为![]() .联立直线的参数方程与二次曲线的方程可得
.联立直线的参数方程与二次曲线的方程可得![]() .
. ![]() .则
.则![]() .
.
详解:(1)因为![]() ,
,
由![]() 得
得![]() ,
,
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由![]() 得
得![]() ,
,
所以曲线![]() 的直角坐标方程为:
的直角坐标方程为: ![]() .
.
(2)不妨设四个交点自下而上依次为![]() ,它们对应的参数分别为
,它们对应的参数分别为![]() .
.
把 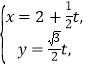 代入
代入![]() ,
,

得![]() ,即
,即![]() ,
,
则![]() ,
,![]() .
.
把 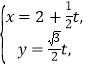 代入
代入![]() ,
,
得![]() ,即
,即![]() , 则
, 则![]() ,
,![]() .
.
所以![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学 | 不喜欢数学 | 总计 | |
男 | 30 | ① | 45 |
女 | ② | 25 | 45 |
总计 | ③ | ④ | 90 |
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐的单音色旋律,选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ) 完成下列2×2列联表;
正误 年龄 | 正确 | 错误 | 合计 |
20~30 | 30 | ||
30~40 | 70 | ||
合计 | 120 |
(Ⅱ)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |