Question

【题目】关于函数,下列说法正确的是（ ）

（1）是的极大值点 ；（2）函数有且只有1个零点；（3）存在正实数，使得恒成立 ；（4）对任意两个正实数，且，若，则

A. B. C. D.

Answer 1

【答案】B

【解析】

依次判断各个选项：（1）利用导数与极值的关系可知是的极小值点，则（1）错误；（2）利用导数研究的单调性，结合零点存在定理判断可知（2）正确；（3）采用分离变量的方式，通过求解的单调性和极限，可判断出，则（3）错误；（4）构造函数，通过导数可求得，从而可确定时，，从而证得结论，知（4）正确.

（1）

当时，，此时单调递减

当时，，此时单调递增

可知是的极小值点，可知（1）错误

（2）

，即在上单调递减

又；

则，使得

由函数单调性可知有且只有个零点，可知（2）正确

（3）若在上恒成立，则

令，则

令，则

时，；时，

即在上单调递减

又时，

不存在正实数，使得恒成立，可知（3）错误

（4）由（1）可知，在上单调递减；在上单调递增

令，

则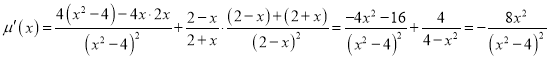

，即在上单调递减

即

，令，由，即

，可知（4）正确

综上所述，说法正确的为：（2）（4）

本题正确选项：