Question

【题目】已知有限集，如果中元素满足，就称为“复活集”.

（1）判断集合是否为“复活集”，并说明理由；

（2）若，，且是“复活集”，求的取值范围；

（3）若，求证：“复活集”有且只有一个，且.

Answer 1

【答案】（1）是；理由见解析；（2）；（3）见解析；

【解析】

根据已知中“复活集”的定义，结合韦达定理及反证法，进而可得答案．

(1)，故集合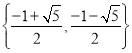是 “复活集”；

(2)不妨设，

则由韦达定理知，是一元二次方程的两个根，

由△，可得，或，或；

(3)不妨设中，

由，得，当时，

即有，

，于是，无解，即不存在满足条件的“复活集” ，

当时，，故只能，，求得，于是“复活集” 只有一个，为，2，．

当时，由，即有，

也就是说“复活集” 存在的必要条件是，事实上，，矛盾，

当时不存在复活集，

所以，“复活集”有且只有一个，且.