题目内容
经过圆x2-4x+y2+2y=0的圆心,且与直线x-2y-3=0平行的直线方程为______.
把圆的方程化为标准方程得:(x-2)2+(y+1)2=5,
∴圆心坐标为(2,-1),
∵所求直线方程与x-2y-3=0平行,
∴所求直线方程的斜率k=
,又所求直线方程过圆心,
则所求直线的方程为:y+1=
(x-2),即x-2y-4=0.
故答案为:x-2y-4=0
∴圆心坐标为(2,-1),
∵所求直线方程与x-2y-3=0平行,
∴所求直线方程的斜率k=
| 1 |
| 2 |
则所求直线的方程为:y+1=
| 1 |
| 2 |
故答案为:x-2y-4=0

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
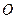 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为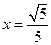 ,离心率
,离心率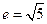 .
.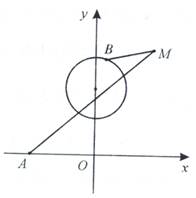
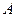 的坐标为
的坐标为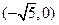 ,
,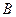 是圆
是圆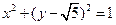 上的点,点
上的点,点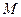 在双曲线右支上,求
在双曲线右支上,求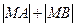 的最小值,并求此时
的最小值,并求此时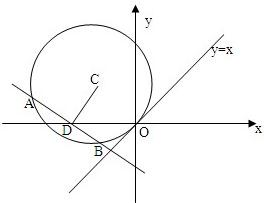
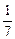 B.-1<t<
B.-1<t< C.-
C.-