题目内容
已知圆心在第二象限,半径为2
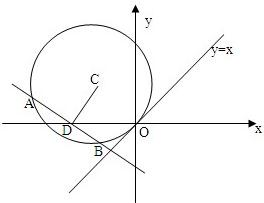
的圆C与直线y=x相切于坐标原点O,过点D(-3,0)作直线l与圆C相交于A,B两点,且|DA|=|DB|.
(1)求圆C的方程;
(2)求直线l的方程.
| 2 |
(1)求圆C的方程;
(2)求直线l的方程.

(1)设圆C的圆心为C(a,b),则圆C的方程为:(x-a)2+(y-b)2=8
∵直线y=x与圆C相切于坐标原点O,∴点O在圆C上,且直线OC垂直于直线y=x
于是有
,
解得
或
,
由圆心C在第二象限得a=-2,b=2,所以圆C的方程为(x+2)2+(y-2)2=8.
(2)由|DA|=|DB|知点D为弦AB的中点,由垂径定理知CD⊥AB,
∵KCD=
=2,
∴KAB=-
,
∵直线l过点D(-3,0),
∴直线l的方程为:y=-
(x+3),
即:x+2y+3=0.
∵直线y=x与圆C相切于坐标原点O,∴点O在圆C上,且直线OC垂直于直线y=x
于是有
|
解得
|
|
由圆心C在第二象限得a=-2,b=2,所以圆C的方程为(x+2)2+(y-2)2=8.
(2)由|DA|=|DB|知点D为弦AB的中点,由垂径定理知CD⊥AB,
∵KCD=
| 2-0 |
| -2+3 |
∴KAB=-
| 1 |
| 2 |
∵直线l过点D(-3,0),
∴直线l的方程为:y=-
| 1 |
| 2 |
即:x+2y+3=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为直径两端点的圆的方程为 。
为直径两端点的圆的方程为 。