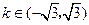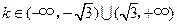题目内容
求过圆:x2+y2-2x+2y+1=0与圆:x2+y2+4x-2y-4=0的交点,圆心在直线:x-2y-5=0的圆的方程.
设所求的圆为C,
∵圆C经过圆x2+y2-2x+2y+1=0与圆x2+y2+4x-2y-4=0的交点,
∴设圆C方程为x2+y2-2x+2y+1+λ(x2+y2+4x-2y-4)=0,
化简得x2+y2+
x+
y+
=0,可得圆心坐标为C(-
,-
).
∵圆心在直线:x-2y-5=0上,
∴-
-2(-
)-5=0,解之得λ=-
.
因此,圆C的方程为x2+y2-
x+
y+
=0,即为所求圆的方程.
∵圆C经过圆x2+y2-2x+2y+1=0与圆x2+y2+4x-2y-4=0的交点,
∴设圆C方程为x2+y2-2x+2y+1+λ(x2+y2+4x-2y-4)=0,
化简得x2+y2+
| 4λ-2 |
| 1+λ |
| 2-2λ |
| 1+λ |
| 1-4λ |
| 1+λ |
| 2λ-1 |
| 1+λ |
| 1-λ |
| 1+λ |
∵圆心在直线:x-2y-5=0上,
∴-
| 2λ-1 |
| 1+λ |
| 1-λ |
| 1+λ |
| 2 |
| 9 |
因此,圆C的方程为x2+y2-
| 26 |
| 7 |
| 22 |
| 7 |
| 17 |
| 7 |

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.
的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.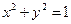 与直线
与直线 没有公共点的充要条件是( )
没有公共点的充要条件是( )