题目内容
【题目】如图，在边长为a的菱形ABCD中，
，E,F分别是PA和AB的中点．
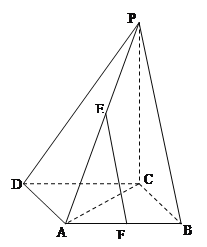
（1）求证： EF||平面PBC；
（2）求E到平面PBC的距离．
【答案】（1）见解析；（2）
.
【解析】
试题（1）根据三角形的中线平行于底边，由线线平行推出线面平行即可；（2）在面ABCD内作过F作
于H，证明
；再根据平行于平面的一条直线上的所有点到平面的距离相等，得点E到平面PBC的距离等于点F到平面PBC的距离FH；在直角三角形FBH中，得
.
试题解析：
（1）证明：∵AE=PE，AF=BF，
∴EF∥PB
又
故
（2）解：在面ABCD内作过F作
又
，
，
又，故点E到平面PBC的距离等于点F到平面PBC的距离FH．
在直角三角形FBH中，
，
故点E到平面PBC的距离等于点F到平面PBC的距离，等于
.
练习册系列答案
相关题目
