题目内容
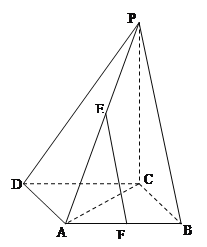
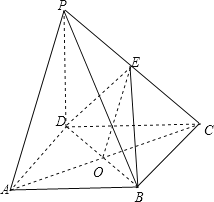
【题目】如图，四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD是边长为a的正方形，且PD=a．
（1）求四棱锥P﹣ABCD的体积；
（2）若E为PC中点，求证：PA∥平面BDE；
（3）求直线PB与平面ABCD所成角的正切值．
【答案】见解析
【解析】解：（1）四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD是边长为a的正方形，且PD=a．
所以：
=
证明：（2）在正方形ABCD中，连接AC和BD交与点O，连接OE，
所以：O是AC的中点，
由于E是PC的中点，
所以：OE是△PAC的中位线，
则：OE∥PA
OE平面BDE
PA平面BDE，
所以：PA∥平面BDE．
解：（3）PD⊥底面ABCD，底面ABCD是边长为a的正方形，且PD=a．
则：BD=
所以：∠PBD就是PB与平面ABCD所成角．
则：
所以：直线PB与平面ABCD所成角的正切值为
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
