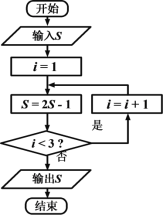
题目内容
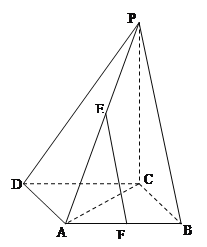
【题目】等腰直角三角形![]() 的斜边AB为正四面体
的斜边AB为正四面体![]() 侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下列说法:
侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下列说法:

(1)四面体E![]() BCD的体积有最大值和最小值;
BCD的体积有最大值和最小值;
(2)存在某个位置,使得![]() ;
;
(3)设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ;
;
(4)AE的中点M与AB的中点N连线交平面BCD于点P,则点P的轨迹为椭圆.
其中,正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析:首先结合正四面体的特征以及等腰直角三角形在旋转的过程中对应的特点,得到相关的信息,结合题中所给的条件,以及相关的结论,认真分析,逐一对比,得到结果.
详解:根据正四面体的特征,以及等腰直角三角形的特征,可以得到当直角边![]() 绕斜边
绕斜边![]() 旋转的过程中,存在着最高点和最低点,并且最低点在底面的上方,所以四面体E
旋转的过程中,存在着最高点和最低点,并且最低点在底面的上方,所以四面体E![]() BCD的体积有最大值和最小值,故(1)正确;
BCD的体积有最大值和最小值,故(1)正确;
要想使![]() ,就要使
,就要使![]() 落在竖直方向的平面内,而转到这个位置的时候,使得满足
落在竖直方向的平面内,而转到这个位置的时候,使得满足![]() ,但是就不满足是等腰直角三角形了,所以(2)不正确;
,但是就不满足是等腰直角三角形了,所以(2)不正确;
利用二面角的平面角的定义,找到其平面角,可以判断得出设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,所以(3)是正确的;
,所以(3)是正确的;
根据平面截圆锥所得的截面可以断定,AE的中点M与AB的中点N连线交平面BCD于点P,则点P的轨迹为椭圆,所以(4)正确;
故正确的命题的个数是3个,故选C.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目