题目内容
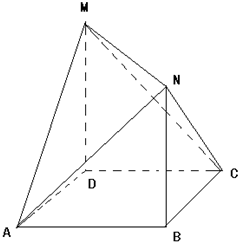 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
| ||
| 2 |
(1)以向量
| AB |
(2)求证:平面AMN⊥平面CMN;
(3)求该几何体的体积.
考点:棱柱、棱锥、棱台的体积,简单空间图形的三视图,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)以向量
方向为侧视方向,能画出侧视图.
(2)取MN中点为O,连AO,CO可证平面AMN⊥平面CMN.
(3)V=VA-BDMN+VC-BDMN,证明出AC⊥平面BDMN,由此能求出该几何体的体积.
| AB |
(2)取MN中点为O,连AO,CO可证平面AMN⊥平面CMN.
(3)V=VA-BDMN+VC-BDMN,证明出AC⊥平面BDMN,由此能求出该几何体的体积.
解答:
(1)解:以向量
方向为侧视方向,画出侧视图,如右图所示.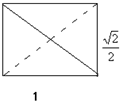 (2分)
(2分)
(2)证明:∵四边形ABCD是边长为1的正方形,
MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
,
∴AM=AN=CM=CN=
=
,MN=AC=
,
取MN中点为O,连AO,CO,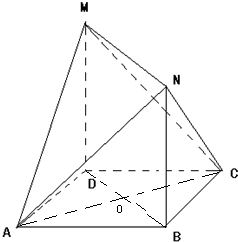
则AO=CO=
=1,AO⊥MN,BO⊥MN,
∴∠AOC是平面AMN和平面CMN所成的二面角的平面角,
∵AO2+CO2=AC2,
∴∠AOC=90°,
∴平面AMN⊥平面CMN.(7分)
(3)解:连结AC,BD,
∵四边形ABCD是边长为1的正方形,MD⊥平面ABCD,
∴AC⊥BD,MD⊥AC,
又BD∩MD=D,∴AC⊥平面BDMN,(9分)
∵S矩形BDMN=BD×MD=
×
=1,AC=
,
∴该几何体的体积V=VA-BDMN+VC-BDMN
=
×
×1
=
.(12分)
| AB |
 (2分)
(2分)(2)证明:∵四边形ABCD是边长为1的正方形,
MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
| ||
| 2 |
∴AM=AN=CM=CN=
1+
|
| ||
| 2 |
| 2 |
取MN中点为O,连AO,CO,

则AO=CO=
|
∴∠AOC是平面AMN和平面CMN所成的二面角的平面角,
∵AO2+CO2=AC2,
∴∠AOC=90°,
∴平面AMN⊥平面CMN.(7分)
(3)解:连结AC,BD,
∵四边形ABCD是边长为1的正方形,MD⊥平面ABCD,
∴AC⊥BD,MD⊥AC,
又BD∩MD=D,∴AC⊥平面BDMN,(9分)
∵S矩形BDMN=BD×MD=
| 2 |
| ||
| 2 |
| 2 |
∴该几何体的体积V=VA-BDMN+VC-BDMN
=
| 1 |
| 3 |
| 2 |
=
| ||
| 3 |
点评:本题考查侧视图的作法,考查平面AMN⊥平面CMN的证明,考查几何体的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知
=(0,1,1),
=(-2,2,0),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
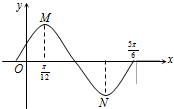 如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<
如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<