题目内容
已知数列{an}的首项为1，且满足an+2-an=a2-a1=1，则数列{an}的前100项和为 ．
考点：数列的求和
专题：等差数列与等比数列
分析：由条件得求出a2，并判断出数列奇数项、偶数项均构成等差数列，利用等差数列的求和公式求出前100项和．
解答：
解：由题意得a1=1，a2-a1=1，所以a2=2，
因为an+2-an=1，
所以数列{an}奇数项构成以1为首项、公差的等差数列，
偶数项构成以2为首项、以1为公差的等差数列，
则前100项和S=（50×1+
×1）+（50×2+
×1）=2600，
故答案为：2600．
因为an+2-an=1，
所以数列{an}奇数项构成以1为首项、公差的等差数列，
偶数项构成以2为首项、以1为公差的等差数列，
则前100项和S=（50×1+
| 50×49 |
| 2 |
| 50×49 |
| 2 |
故答案为：2600．
点评：本题考查了等差数列的定义、前n项和公式的应用，难度不大．
练习册系列答案
相关题目
已知△ABC不是直角三角形，三个角∠A、∠B、∠C对应的边分别是a、b、c，记ωA=
•
，ωB=
•
，ωC=
•
，下列结论中，错误的是（ ）
| AB |
| AC |
| BC |
| BA |
| CA |
| CB |
| A、ωA+ωB=c2 |
| B、ωAωBωC=-（abc）2 |
| C、若ωA=ωB=ωC，则△ABC为等边三角形 |
| D、ωAtanA=ωBtanB=ωCtanC |
在△ABC中，a2+b2-c2=
ab，则角C为（ ）
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
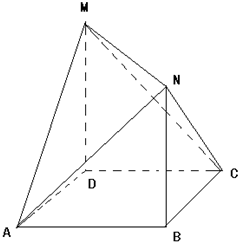如图，四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD=NB=