题目内容
已知
=(0,1,1),
=(-2,2,0),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
考点:空间向量的夹角与距离求解公式
专题:空间向量及应用
分析:由空间向量的夹角公式计算可得.
解答:
解:设向量
与
的夹角为θ,0°≤θ≤180°,
∵
=(0,1,1),
=(-2,2,0),
∴cosθ=
=
=
∴向量
与
的夹角θ为60°
故选:C
| a |
| b |
∵
| a |
| b |
∴cosθ=
| ||||
|
|
| 0×(-2)+1×2+1×0 | ||||
|
| 1 |
| 2 |
∴向量
| a |
| b |
故选:C
点评:本题考查空间向量的夹角公式,属基础题.

练习册系列答案
相关题目
在△ABC中,a2+b2-c2=
ab,则角C为( )
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |
从6人中选4人分别到省内黄果树、小七孔、西江苗寨、梵净山游览,要求每个地点有一人游览,每人只游览一个地点,且在这6人中甲、乙不去西江苗寨游览,则不同的选择方案共有( )
| A、300种 | B、240种 |
| C、144种 | D、96种 |
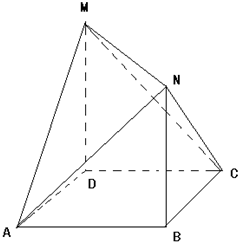 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=