题目内容
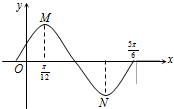 如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<
如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<| π |
| 2 |
| OM |
| ON |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质,平面向量及应用
分析:首先利用函数的周期确定ω的值,进一步利用向量的数量积确定A的值.
解答:
解:根据函数的图象:
=
-
=
T=π
则:ω=2
M、N分别是最大、最小值点,且
⊥
则:M(
,A),N(
,-A)
所以利用向量的数量积解得:
A=
故答案为:ω=2,A=
| 3T |
| 4 |
| 5π |
| 6 |
| π |
| 12 |
| 3π |
| 4 |
T=π
则:ω=2
M、N分别是最大、最小值点,且
| OM |
| ON |
则:M(
| π |
| 12 |
| 7π |
| 12 |
所以利用向量的数量积解得:
A=
| ||
| 12 |
故答案为:ω=2,A=
| ||
| 12 |
点评:本题考查的知识要点:利用函数的图象的周期,向量的数量积求函数的解析式,属于基础题型.

练习册系列答案
相关题目
在△ABC中,a2+b2-c2=
ab,则角C为( )
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
若函数f(x)=x3-mx2+mx+3m在(0,1)内有极大值,无极小值,则( )
| A、m<0 | B、m<3 |
| C、m>3 | D、0<m<3 |
已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |
设全集U={x∈N*|x<6},集合A={1,3},B={1,3,5},则∁U(A∪B)等于( )
| A、{1,4} |
| B、{1,5} |
| C、{2,5} |
| D、{2,4} |
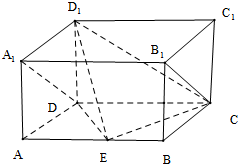 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.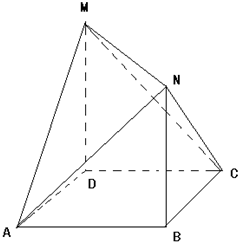 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=