题目内容
在极坐标系中,已知曲线C的方程为ρ2cos2θ=4,过点(1,π)的直线l与直线θ=
(ρ∈R)平行,现以极点为原点,极轴为x轴正半轴建立平面直角坐标系,
(1)在该直角坐标系下,求曲线C和直线l的直角坐标方程;
(2)判断直线l与曲线C的位置关系,若相交,则求出弦长;若相切,则求出切点坐标;若相离,则求出曲线C上的点到直线l的距离的最小值.
| π |
| 6 |
(1)在该直角坐标系下,求曲线C和直线l的直角坐标方程;
(2)判断直线l与曲线C的位置关系,若相交,则求出弦长;若相切,则求出切点坐标;若相离,则求出曲线C上的点到直线l的距离的最小值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)由曲线C的方程为ρ2cos2θ=4,可得ρ2cos2θ-ρ2sin2θ=4,可得曲线C的直角坐标方程为x2-y2=4.又直线θ=
(ρ∈R)的斜率k=tan
=
.点(1,π)的直角坐标为(-1,0).利用点斜式可得可得直线l的直角坐标方程.
(2)直线方程与双曲线方程联立可得2x2-2x-13=0,此时△>0,直线l与曲线C相交,设直线l与曲线C两个交点分别为A(x1,y1),B(x2,y2).利用根与系数的关系与
弦长|AB|=
•
即可得出.
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
(2)直线方程与双曲线方程联立可得2x2-2x-13=0,此时△>0,直线l与曲线C相交,设直线l与曲线C两个交点分别为A(x1,y1),B(x2,y2).利用根与系数的关系与
弦长|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
解答:
解:(1)∵曲线C的方程为ρ2cos2θ=4,∴ρ2cos2θ-ρ2sin2θ=4,
∴曲线C的直角坐标方程为x2-y2=4.
又∵直线θ=
(ρ∈R)的斜率k=tan
=
.
点(1,π)的直角坐标为(-1,0).
∴直线l的直角坐标方程为y=
(x+1).
(2)由
可得2x2-2x-13=0,
∵此时△=(-2)2-4×2×(-13)>0,
∴直线l与曲线C相交,
设直线l与曲线C两个交点分别为A(x1,y1),B(x2,y2).
则x1+x2=1,x1x2=-
.
∴弦长|AB|=
•
=
•
=6.
∴曲线C的直角坐标方程为x2-y2=4.
又∵直线θ=
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
点(1,π)的直角坐标为(-1,0).
∴直线l的直角坐标方程为y=
| ||
| 3 |
(2)由
|
∵此时△=(-2)2-4×2×(-13)>0,
∴直线l与曲线C相交,
设直线l与曲线C两个交点分别为A(x1,y1),B(x2,y2).
则x1+x2=1,x1x2=-
| 13 |
| 2 |
∴弦长|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
1+
|
| 1+26 |
点评:本题考查了极坐标化为直角坐标方程、直线与双曲线的相交转化为方程联立可得根与系数的关系、弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,a2+b2-c2=
ab,则角C为( )
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
已知双曲线
-
=1的一个焦点在圆x2+y2-4x-5=0上,则双曲线的离心率为( )
| x2 |
| 9 |
| y2 |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从6人中选4人分别到省内黄果树、小七孔、西江苗寨、梵净山游览,要求每个地点有一人游览,每人只游览一个地点,且在这6人中甲、乙不去西江苗寨游览,则不同的选择方案共有( )
| A、300种 | B、240种 |
| C、144种 | D、96种 |
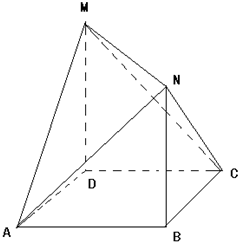 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
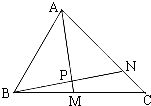 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.