题目内容
已知△ABC中,AB=2,BC=1,∠ABC=90°,平面ABC外一点,P满足PA=PB=PC=
,则三棱锥P-ABC的体积是( )
| 3 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知得棱锥顶点P在底面投影为△ABC的外心,CA=
,外接圆半径R=
=
,高h=
=1,S△ABC=
×2×1=1,由此能求出三棱椎P-ABC的体积.
| 5 |
| CA |
| 2sin90° |
| ||
| 2 |
(
|
| 1 |
| 2 |
解答:
解:∵PA=PB=PC=
,
∴棱锥顶点P在底面投影为△ABC的外心
∴先求外接圆半径R,
∵CA2=22+12-2•2•1cos90°=5,CA=
,
∴R=
=
,
∴高h=
=1,
S△ABC=
×2×1=1,
三棱椎P-ABC的体积V=
×1×1=
.
故选:B.
| 3 |
| 2 |
∴棱锥顶点P在底面投影为△ABC的外心
∴先求外接圆半径R,
∵CA2=22+12-2•2•1cos90°=5,CA=
| 5 |
∴R=
| CA |
| 2sin90° |
| ||
| 2 |
∴高h=
(
|
S△ABC=
| 1 |
| 2 |
三棱椎P-ABC的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
故选:B.
点评:本题考查三棱锥的体积的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
设全集U={x∈N*|x<6},集合A={1,3},B={1,3,5},则∁U(A∪B)等于( )
| A、{1,4} |
| B、{1,5} |
| C、{2,5} |
| D、{2,4} |
若sinx•cosx=
,且
<x<
,则cosx-sinx的值是( )
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|
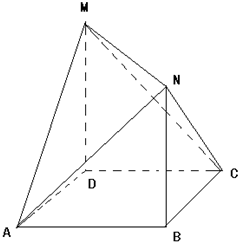 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=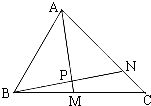 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.