题目内容
函数f(x)=ax(a>0且a≠1)在区间[1,2]上的最大值比最小值大
,则实数a的值为 .
| a |
| 4 |
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:讨论指数函数y=ax(a>0且a≠1)的单调性,从而确定函数的最值,从而求a.
解答:
解:由题意可得:
∵当a>1时,函数f(x)在区间[1,2]上单调递增,
∴f(2)-f(1)=a2-a=
,解得a=0(舍去),或a=
.
∵当 0<a<1时,函数f(x)在区间[1,2]上单调递减,
∴f(1)-f(2)=a-a2=
,解得a=0(舍去),或a=
.
故答案为:
或
;
∵当a>1时,函数f(x)在区间[1,2]上单调递增,
∴f(2)-f(1)=a2-a=
| a |
| 4 |
| 5 |
| 4 |
∵当 0<a<1时,函数f(x)在区间[1,2]上单调递减,
∴f(1)-f(2)=a-a2=
| a |
| 4 |
| 3 |
| 4 |
故答案为:
| 5 |
| 4 |
| 3 |
| 4 |
点评:本题主要考查指数函数的单调性的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |
从6人中选4人分别到省内黄果树、小七孔、西江苗寨、梵净山游览,要求每个地点有一人游览,每人只游览一个地点,且在这6人中甲、乙不去西江苗寨游览,则不同的选择方案共有( )
| A、300种 | B、240种 |
| C、144种 | D、96种 |
下列说法正确的是( )
| A、在散点图中看不出两个变量是正相关还是负相关 |
| B、回归方程得到的预报值是预报变量的精确值 |
| C、回归方程一般都有时间性 |
| D、相关系数r越接近0,说明两个变量的线性相关性越强 |
设全集U={x∈N*|x<6},集合A={1,3},B={1,3,5},则∁U(A∪B)等于( )
| A、{1,4} |
| B、{1,5} |
| C、{2,5} |
| D、{2,4} |
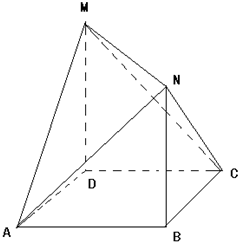 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=