题目内容
若曲线y=xlnx在点P处的切线过点（0，-1），则点P的坐标 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用,直线与圆
分析：求出函数的导数，设出切点，求出切线的斜率，再由两点的斜率公式，解方程，即可得到切点．
解答：
解：y=xlnx的导数y′=lnx+1（x＞0），
设切点P（m，n），则在点P处的切线斜率为：1+lnm，
则n=mlnm，1+lnm=
，
解得，m=1，n=0．
即有P（1，0）．
故答案为：（1，0）．
设切点P（m，n），则在点P处的切线斜率为：1+lnm，
则n=mlnm，1+lnm=
| n+1 |
| m |
解得，m=1，n=0．
即有P（1，0）．
故答案为：（1，0）．
点评：本题考查导数的几何意义：曲线在该点处的切线的斜率，考查直线的斜率公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知△ABC不是直角三角形，三个角∠A、∠B、∠C对应的边分别是a、b、c，记ωA=
•
，ωB=
•
，ωC=
•
，下列结论中，错误的是（ ）
| AB |
| AC |
| BC |
| BA |
| CA |
| CB |
| A、ωA+ωB=c2 |
| B、ωAωBωC=-（abc）2 |
| C、若ωA=ωB=ωC，则△ABC为等边三角形 |
| D、ωAtanA=ωBtanB=ωCtanC |
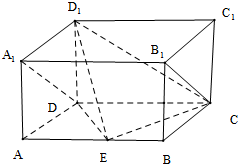如图，长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E是AB的中点．
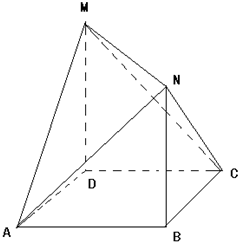如图，四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD=NB=