题目内容
18.设P是曲线y=$\sqrt{1{-x}^{2}}$上的点,若对曲线y=x+$\frac{a}{x}$(a>0,x>0)上的任意一点Q,恒有|PQ|≥1,则a的取值范围是( )| A. | [$\sqrt{2}$-1,+∞) | B. | [2$\sqrt{2}$-2,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | (0,2$\sqrt{2}$-2] |
分析 由题意,曲线y=x+$\frac{a}{x}$(a>0,x>0)上的任意一点Q,恒有|OQ|≥2,可得2x4+(2a-4)x2+a2≥0,换元,利用判别式,即可得出结论.
解答 解:由题意,曲线y=x+$\frac{a}{x}$(a>0,x>0)上的任意一点Q,恒有|OQ|≥2,
∴$\sqrt{{x}^{2}+(x+\frac{a}{x})^{2}}$≥2,
∴2x4+(2a-4)x2+a2≥0,
令t=x2,则2t2+(2a-4)t+a2≥0在(0,+∞)上恒成立,
∴△=(2a-4)2-8a2≤0或1-a<0,
∵a>0,
∴a≥2$\sqrt{2}$-2,
故选:B.
点评 本题考查直线与圆的位置关系,考查学生分析解决问题的能力,正确转化是关键.

练习册系列答案
相关题目
9.记关于x的不等式$\frac{x-a}{x+1}<0$的解集为P,不等式|x-1|≤1的解集为Q,若Q⊆P,求正数a的取值范围( )
| A. | (2,+∞) | B. | (-∞,-2) | C. | [2,+∞) | D. | (-∞,-2] |
13.向量$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(n,-1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则mn=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
3.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°,则$\vec b•(\vec b-\vec a)$等于( )
| A. | 1 | B. | 3 | C. | 2-$\sqrt{3}$ | D. | 4-$\sqrt{3}$ |
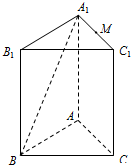 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.