题目内容
13．向量$\overrightarrow{a}$=（m，2），$\overrightarrow{b}$=（n，-1），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则mn=（ ）| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
分析 由向量垂直数量积为0 得到关于mn的等式．
解答 解：因为向量$\overrightarrow{a}$=（m，2），$\overrightarrow{b}$=（n，-1），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，所以$\overrightarrow{a}•\overrightarrow{b}$=0，即mn-2=0，所以mn=2；
故选：C．
点评 本题考查了向量垂直，数量积为0．属于基础题．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
3．函数f（x）=$\frac{\sqrt{2x+1}}{x-3}$的定义域为（ ）
| A． | {x|x≥-$\frac{1}{2}$} | B． | {x|x＞-$\frac{1}{2}$且x≠3} | C． | {x|x≥-$\frac{1}{2}$且x≠3} | D． | {x|x≠3} |
4．
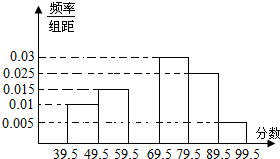如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布表和频率分布直方图如下，回答下列问题：
（1）分别求出a，b，x，y的值，并补全频率分布直方图；
（2）估计这次环保知识竞赛平均分；
（3）若从所有参加环保知识竞赛的学生中随机抽取一人采访，抽到的学生成绩及格的概率有多大？
如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布表和频率分布直方图如下，回答下列问题：| 分组 | 人数 | 频率 |
| [39.5，49.5） | a | 0.10 |
| [49.5，59.5） | 9 | x |
| [59.5，69.5） | b | 0.15 |
| [69.5，79.5） | 18 | 0.30 |
| [79.5，89.5） | 15 | y |
| [89.5，99.5] | 3 | 0.05 |
（2）估计这次环保知识竞赛平均分；
（3）若从所有参加环保知识竞赛的学生中随机抽取一人采访，抽到的学生成绩及格的概率有多大？
1．已知线段PQ的中点为M（0，4），若点P在直线x+y-2=0上运动，则点Q的轨迹方程是（ ）
| A． | x+y-6=0 | B． | x+y+6=0 | C． | x-y-2=0 | D． | x-y+2=0 |
8．将编号为1、2、3、4的四个小球任意地放入A、B、C、D四个小盒中，每个盒中放球的个数不受限制，恰好有一个盒子是空的概率为（ ）
| A． | $\frac{9}{16}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{16}$ |
18．设P是曲线y=$\sqrt{1{-x}^{2}}$上的点，若对曲线y=x+$\frac{a}{x}$（a＞0，x＞0）上的任意一点Q，恒有|PQ|≥1，则a的取值范围是（ ）
| A． | [$\sqrt{2}$-1，+∞） | B． | [2$\sqrt{2}$-2，+∞） | C． | [$\frac{4}{5}$，+∞） | D． | （0，2$\sqrt{2}$-2] |
5．函数$y=cos（x+\frac{π}{12}）$的图象的一条对称轴的方程是（ ）
| A． | $x=\frac{5π}{12}$ | B． | x=$\frac{π}{6}$ | C． | x=$\frac{π}{12}$ | D． | x=-$\frac{π}{12}$ |
2．为了得到函数$y={（\frac{1}{3}）^x}$的图象，可以把函数$y=3×{（\frac{1}{3}）^x}$的图象（ ）
| A． | 向左平移1个单位 | B． | 向右平移1个单位 | C． | 向左平移3个单位 | D． | 向右平移3个单位 |