题目内容
8.已知函数f(x)=-2x2+bx+c,当x=1时有最大值1.(1)若方程|f(x)|=m有4个不同实根,求实数m的取值范围,并求这4个实根的和;
(2)当x∈[m,n](0<m<n)时,f(x)取值范围为[$\frac{1}{n}$,$\frac{1}{m}$],试求m,n的值.
分析 (1)由题意可得$\frac{b}{4}$=1,f(1)=-2+b+c=1,从而解出f(x)=-2x2+4x-1;在同一坐标系中分别作出函数y=|f(x)|与y=m的图象,利用数形结合求解.
(2)因为当x∈R时,f(x)最大值为1,所以$\frac{1}{m}$≤1,m≥1,从而可得$\left\{\begin{array}{l}{f(m)=\frac{1}{m}}\\{f(n)=\frac{1}{n}}\end{array}\right.$,从而可得(x-1)(2x2-2x-1)=0,从而解得m=1,n=$\frac{1+\sqrt{3}}{2}$.
解答 解:(1)由已知得$\frac{b}{4}$=1,f(1)=-2+b+c=1,
解得b=4,c=-1;
即f(x)=-2x2+4x-1;
在同一坐标系中分别作出函数y=|f(x)|与y=m的图象如下,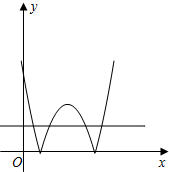
由图象知,当0<m<1时,
两函数y=|f(x)|与y=m的图象有4个不同交点,且分别是关于直线x=1对称的两对对称点,
所以方程|f(x)=m有4个不同实根,
这4个不同实根的和为4.
(2)因为当x∈R时,f(x)最大值为1,所以$\frac{1}{m}$≤1,m≥1,
所以当x∈[m,n](0<m<n)时,f(x)单调递减,
于是有$\left\{\begin{array}{l}{f(m)=\frac{1}{m}}\\{f(n)=\frac{1}{n}}\end{array}\right.$,
所以f(x)=$\frac{1}{x}$在[1,+∞)上有两个不等的实根m,n,
且n>m≥1,
由f(x)=$\frac{1}{x}$得-2x2+4x-1=$\frac{1}{x}$,
2x3-4x2+x+1=0,
(x-1)(2x2-2x-1)=0,
解之得x1=1,x2=$\frac{1+\sqrt{3}}{2}$,x3=$\frac{1-\sqrt{3}}{2}$,
所以m=1,n=$\frac{1+\sqrt{3}}{2}$.
点评 本题考查了函数的性质的化简与应用,同时考查了数形结合的思想应用,属于中档题.

| A. | [$\sqrt{2}$-1,+∞) | B. | [2$\sqrt{2}$-2,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | (0,2$\sqrt{2}$-2] |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 取到的球的个数 | B. | 取到红球的个数 | ||
| C. | 至少取到一个红球 | D. | 至少取到一个红球的概率 |