题目内容

3．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°，则$\vec b•（\vec b-\vec a）$等于（　　）
A．1B．3C．2-$\sqrt{3}$D．4-$\sqrt{3}$

分析 将所求展开，利用已知得到数量积，可求．

解答 解：因为|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°，则$\vec b•（\vec b-\vec a）$=${\overrightarrow{b}}^{2}-\overrightarrow{b}•\overrightarrow{a}$=4-1×2×cos60°=3；
故选B．

点评 本题考查了平面向量的数量积公式的运用；属于基础题．

练习册系列答案
相关题目
13．设$\overrightarrow{a}$，$\overrightarrow{b}$是两个非零向量，且|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为（　　）
A．120°B．90°C．60°D．30°
14．已知函数f（x）=a（x-1）2+lnx，a∈R．
（Ⅰ）当a=-$\frac{1}{4}$时，求函数y=f（x）的单调区间；
（Ⅱ）a=$\frac{1}{2}$时，令h（x）=f（x）-3lnx+x-$\frac{1}{2}$．求h（x）在[1，e]上的最大值和最小值；
（Ⅲ）若函数f（x）≤x-1对?x∈[1，+∞）恒成立，求实数a的取值范围．
11．设集合M={1，3}，N={1，2，3}，则M∪N=（　　）
A．{2}B．{1，2}C．{1，3}D．{1，2，3}
18．设P是曲线y=$\sqrt{1{-x}^{2}}$上的点，若对曲线y=x+$\frac{a}{x}$（a＞0，x＞0）上的任意一点Q，恒有|PQ|≥1，则a的取值范围是（　　）
A．[$\sqrt{2}$-1，+∞）B．[2$\sqrt{2}$-2，+∞）C．[$\frac{4}{5}$，+∞）D．（0，2$\sqrt{2}$-2]
8．阅读如图的程序框图．若输入n=1，则输出k的值为（　　）
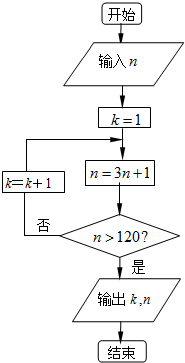
A．3B．4C．5D．6
15．把座位编号为1，2，3，4，5，6的6张电影票分给甲、乙、丙、丁四个人，每人至少分一张，至多分两张，且分得的两张票必须是连号，那么不同分法种数为（　　）
A．240B．144C．196D．288
12．把函数y=sinx的图象上所有点向右平移$\frac{π}{3}$个单位，再将图象上所有点的横坐标缩小到原来的$\frac{1}{2}$（纵坐标不变），所得函数解析式为y=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜0），则（　　）
A．ω=2，φ=-$\frac{π}{3}$B．ω=2，φ=-$\frac{π}{6}$C．ω=$\frac{1}{2}，φ=-\frac{π}{6}$D．ω=$\frac{1}{2}，φ=-\frac{π}{3}$
4．如图几何体中，正视图、侧视图都为长方形的几何体有（　　）
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网