题目内容
6.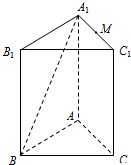 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.(Ⅰ)求证:AC⊥BA1;
(Ⅱ)若M为A1C1的中点,问棱AB上是否存在点N,使得MN∥平面BCC1B1?若存在,求出$\frac{A{N}_{1}}{NB}$的值,并给出证明;若不存在,请说明理由.
分析 解法一:(Ⅰ)由AA1⊥平面ABC,可证AA1⊥AC,又AB⊥AC,可证AC⊥平面ABB1A1.从而得证AC⊥A1B.
(Ⅱ)取AC得中点E,连接MN,ME,NE,可证ME∥CC1.从而可得ME∥平面BCC1B1.又可证NE∥BC,NE∥平面BCC1B1.即可证明平面MNE∥平面BCC1B1.从而可证MN∥平面BCC1B1.
解法二:(Ⅰ)由题意易证平面ABB1A1⊥平面ABC,且平面ABB1A1∩平面ABC=AB.从而AC⊥AB,可证AC⊥平面ABB1A1.即可证明AC⊥A1B.
(Ⅱ)取BC得中点F,连接MN,NF,C1F.可得NF∥AC,NF=$\frac{1}{2}$AC.由MC1∥AC,MC1=$\frac{1}{2}$AC,可证四边形MNFC1为平行四边形.即可证明MN∥C1F.从而判定MN∥平面C1F.
解答 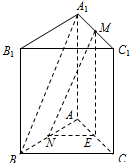 (本题满分12分)
(本题满分12分)
解:解法一:(Ⅰ)∵AA1⊥平面ABC,AC?平面ABC,
∴AA1⊥AC.(2分)
∵AB⊥AC,AB∩AA1=A,
∴AC⊥平面ABB1A1.(4分)
又∵A1B?平面ABB1A1,
∴AC⊥A1B.(5分)
(Ⅱ)存在点N为AB的中点,即$\frac{AN}{NB}=1$,使得MN∥平面BCC1B1.(6分)
证明:取AC得中点E,连接MN,ME,NE
∵四边形ACC1A1是平行四边形,
且M,E分别为A1C1、AC的中点,
∴四边形ECC1M是平行四边形
∴ME∥CC1.(7分)
∵ME?平面BCC1B1,CC1?平面BCC1B1,
∴ME∥平面BCC1B1.(8分)
∵N,E分别为AB、AC的中点,
∴NE∥BC.(9分)
∵NE?平面BCC1B1,BC?平面BCC1B1,
∴NE∥平面BCC1B1.(10分)
∵ME∩NE=E,
∴平面MNE∥平面BCC1B1.(11分)
(注:直接由两组相交线平行得面面平行,扣2分)
∵MN?平面MNE,
∴MN∥平面BCC1B1.(12分)
解法二:(Ⅰ)∵AA1⊥平面ABC,AA1?平面ABB1A1,
∴平面ABB1A1⊥平面ABC,且平面ABB1A1∩平面ABC=AB.(2分)
∵AC⊥AB,AC?平面ABC,
∴AC⊥平面ABB1A1.(4分)
又∵A1B?平面ABB1A1,
∴AC⊥A1B.(5分)
(Ⅱ)存在点N为AB的中点,即$\frac{AN}{NB}=1$,使得MN∥平面BCC1B1.(6分)
证明:取BC得中点F,连接MN,NF,C1F.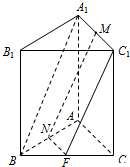
∵N,F分别为AB、BC的中点,
∴NF∥AC,NF=$\frac{1}{2}$AC.(7分)
∵MC1∥AC,MC1=$\frac{1}{2}$AC,
∴MC1∥NF,MC1=NF.(8分)
∴四边形MNFC1为平行四边形.(10分)
∴MN∥C1F.(11分)
∵MN?平面BCC1B1,C1F?平面BCC1B1,
∴MN∥平面C1F.(12分)
点评 本题主要考查了直线与平面垂直的性质,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | x+y-6=0 | B. | x+y+6=0 | C. | x-y-2=0 | D. | x-y+2=0 |
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
| A. | [$\sqrt{2}$-1,+∞) | B. | [2$\sqrt{2}$-2,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | (0,2$\sqrt{2}$-2] |
| A. | 240 | B. | 144 | C. | 196 | D. | 288 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |