题目内容
【题目】如图,正方体ABCD﹣A1B1C1D1中,M,N分别为AB,BC的中点.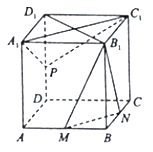
(1)求证:平面B1MN⊥平面BB1D1D;
(2)当点P在DD1上运动时,是否都有MN∥平面A1C1P,证明你的结论;
(3)若P是D1D的中点,试判断PB与平面B1MN是否垂直?请说明理由.
【答案】
(1)证明:连接AC,则AC⊥BD,
又M,N分别是AB,BC的中点,
∴MN∥AC,∴MN⊥BD.
∵ABCD﹣A1B1C1D1是正方体,∴BB1⊥平面ABCD,
∵MN平面ABCD,∴BB1⊥MN,
∵BD∩BB1=B,∴MN⊥平面BB1D1D,
∵MN平面B1MN,
∴平面B1MN⊥平面BB1D1D.
(2)当点P在DD1上移动时,都有MN∥平面A1C1P.
证明如下:
在正方体ABCD﹣A1B1C1D1中,AA1=CC1,AA1∥CC1
∴四边形AA1C1C是平行四边形,
∴AC∥A1C1
由(1)知MN∥AC,
∴MN∥A1C1
又∵MN面A1C1P,A1C1平面A1C1P,
∴MN∥平面A1C1P;
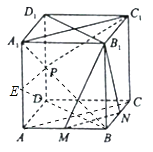
(3)证明:过点P作PE⊥AA1,则PE∥DA,连接BE,
∵DA⊥平面ABB1A1,∴PE⊥平面ABB1A1,即PE⊥B1M,
又∵BE⊥B1M,∴B1M⊥平面PEB,
∴PB⊥MB1,
由(1)中MN⊥平面DD1B1B,得PB⊥MN,
所以PB⊥平面MNB1.
【解析】1、由已知可得BB1⊥平面ABCD,根据线面垂直的判定定理可得证MN⊥平面BB1D1D,即得证平面B1MN⊥平面BB1D1D。
2、根据线面平行的判定定理可得证,当点P在DD1上移动时,都有MN∥平面A1C1P。
3、根据题意作辅助线:过点P作PE⊥AA1,则PE∥DA,连接BE,由已知可得证,PE⊥B1M。再由线面垂直的性质定理得到PB⊥MB1利用(1)的结论可得PB⊥MN,根据线面垂直的判定定理可得证PB⊥平面MNB1.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案