题目内容
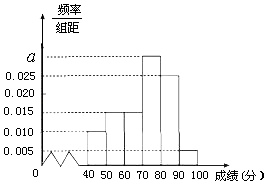
【题目】2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)后得到如图所示的频率分布直方图.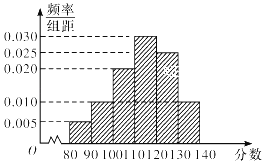
(1)求这40名学生中数学成绩不低于120分的学生人数;
(2)若从数学成绩[80,100)内的学生中任意抽取2人,求成绩在[80,90)中至少有一人的概率.
【答案】
(1)解:由频率分上方图得:
这40名学生中数学成绩不低于120分的学生所占频率为:(0.025+0.010)×10=0.35,
∴这40名学生中数学成绩不低于120分的学生人数为40×0.35=14人
(2)解:从图中知,成绩在[80,90)的人数为m1=0.005×10×40=2(人),
成绩在[90,100)的人数为m2=0.010×10×40=4(人),
设成绩在[80,90)的学生记为a,b,成绩在[90,100)的学生记为c,d,e,f.
则从成绩在[80,100)内的学生中任取2人组成的基本事件有:
(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(d,f),
(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15种.
其中成绩在[80,90)的学生至少有一人的基本事件有:
(a,b),(a,c),(a,d),(a,e),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),共9种.
∴成绩在[80,90)的学生至少有一人的概率为p= ![]() =
= ![]() .
.
【解析】(1)由频率分布直方图求出这40名学生中数学成绩不低于120分的学生所占频率,由此再计算出这40名学生中数学成绩不低于120分的学生人数,(2)求出成绩在[80,90)的人数为2人,成绩在[90,100)的人数为4人,用列举法可得从成绩在[80,100)内的学生中任取2人组成的基本事件有15种,其中成绩在[80,90)的学生至少有一人的基本事件有9种,即可得出概率.
【考点精析】关于本题考查的频率分布表,需要了解第一步,求极差;第二步,决定组距与组数;第三步,确定分点,将数据分组;第四步,列频率分布表才能得出正确答案.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案