题目内容
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)= ![]() .
.
(1)求a、b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上恒成立,求实数k的取值范围;
(3)若f(|2x﹣1|)+k ![]() ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围.
【答案】
(1)解:函数g(x)=ax2﹣2ax+b+1=a(x﹣1)2+1+b﹣a,
因为a>0,所以g(x)在区间[2,3]上是增函数,
故 ![]() ,
,
即 ![]() ,
,
解得 ![]()
(2)解:由已知可得f(x)=x+ ![]() ﹣2,
﹣2,
所以,不等式f(2x)﹣k2x≥0可化为 2x+ ![]() ﹣2≥k2x,
﹣2≥k2x,
可化为 1+( ![]() )2﹣2
)2﹣2 ![]() ≥k,令t=
≥k,令t= ![]() ,则 k≤t2﹣2t+1.
,则 k≤t2﹣2t+1.
因 x∈[﹣1,1],故 t∈[ ![]() ,2].故k≤t2﹣2t+1在t∈[
,2].故k≤t2﹣2t+1在t∈[ ![]() ,2]上恒成立.
,2]上恒成立.
记h(t)=t2﹣2t+1,因为 t∈[ ![]() ,2],故 h(t)min=h(1)=0,
,2],故 h(t)min=h(1)=0,
所以k的取值范围是(﹣∞,0]
(3)解:方程f(|2x﹣1|)+k ![]() ﹣3k=0可化为:
﹣3k=0可化为:
|2x﹣1|2﹣(2+3k)|2x﹣1|+(1+2k)=0,|2x﹣1|≠0,
令|2x﹣1|=t,则方程化为
t2﹣(2+3k)t+(1+2k)=0(t≠0),
∵方程f(|2k﹣1|)+k ![]() ﹣3k=0有三个不同的实数解,
﹣3k=0有三个不同的实数解,
∴由t=|2x﹣1|的图象知,
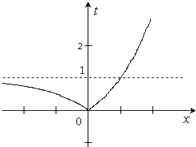
t2﹣(2+3k)t+(1+2k)=0(t≠0),有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1.
记h(t)=t2﹣(2+3k)t+(1+2k),
则 ![]() ,或
,或 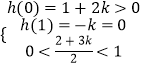
∴k>0.
【解析】(1)由函数g(x)=a(x﹣1)2+1+b﹣a,a>0,所以g(x)在区间[2,3]上是增函数,故 ![]() ,由此解得a、b的值.(2)不等式可化为 2x+
,由此解得a、b的值.(2)不等式可化为 2x+ ![]() ﹣2≥k2x , 故有 k≤t2﹣2t+1,t∈[
﹣2≥k2x , 故有 k≤t2﹣2t+1,t∈[ ![]() ,2],求出h(t)=t2﹣2t+1的最小值,从而求得k的取值范围.(3)方程f(|2x﹣1|)+k
,2],求出h(t)=t2﹣2t+1的最小值,从而求得k的取值范围.(3)方程f(|2x﹣1|)+k ![]() ﹣3k=0|2x﹣1|2﹣(2+3k)|2x﹣1|+(1+2k)=0,(|2x﹣1|≠0),令|2x﹣1|=t,则t2﹣(2+3k)t+(1+2k)=0(t≠0),构造函数h(t)=t2﹣(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围.
﹣3k=0|2x﹣1|2﹣(2+3k)|2x﹣1|+(1+2k)=0,(|2x﹣1|≠0),令|2x﹣1|=t,则t2﹣(2+3k)t+(1+2k)=0(t≠0),构造函数h(t)=t2﹣(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围.
【考点精析】关于本题考查的函数的零点与方程根的关系,需要了解二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能得出正确答案.

【题目】某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 的
的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.