Question

【题目】如图，四边形ABCD是矩形，平面ABCD⊥平面BCE，BE⊥EC．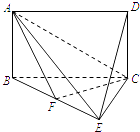

（1）求证：平面AEC⊥平面ABE；
（2）点F在BE上．若DE∥平面ACF，求 的值．

Answer 1

【答案】
（1）证明：因为ABCD为矩形，所以AB⊥BC．

因为平面ABCD⊥平面BCE，平面ABCD∩平面BCE=BC，AB平面ABCD，

所以AB⊥平面BCE．

因为CE平面BCE，所以CE⊥AB．

因为CE⊥BE，AB平面ABE，BE平面ABE，AB∩BE=B，

所以CE⊥平面ABE．

因为CE平面AEC，所以平面AEC⊥平面ABE

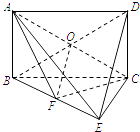
（2）解：连接BD交AC于点O，连接OF．

因为DE∥平面ACF，DE平面BDE，平面ACF∩平面BDE=OF，

所以DE∥OF．

又因为矩形ABCD中，O为BD中点，

所以F为BE中点，即 = ．

【解析】（1）根据平面ABCD⊥平面BCE，利用面面垂直的性质可得AB⊥平面BCE，从而可得CE⊥AB，由CE⊥BE，根据线面垂直的判定可得CE⊥平面ABE，从而可得平面AEC⊥平面ABE；（2）连接BD交AC于点O，连接OF．根据DE∥平面ACF，可得DE∥OF，根据O为BD中点，可得F为BE中点，从而可得结论．
【考点精析】利用直线与平面平行的性质和平面与平面垂直的判定对题目进行判断即可得到答案，需要熟知一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行；一个平面过另一个平面的垂线，则这两个平面垂直．