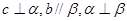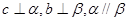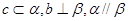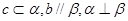题目内容
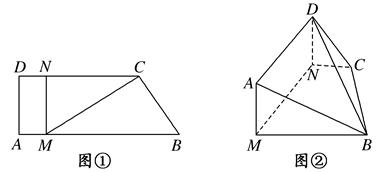
(14分)如图①,直角梯形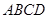 中,
中,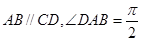 ,点
,点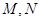 分别在
分别在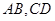 上,且
上,且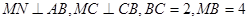 ,现将梯形
,现将梯形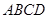 A沿
A沿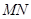 折起,使平面
折起,使平面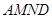 与平面
与平面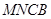 垂直(如图②).
垂直(如图②).
(1)求证: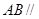 平面
平面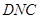 ;
;
(2)当 时,求二面角
时,求二面角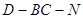 的大小.
的大小.
 中,
中,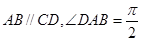 ,点
,点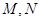 分别在
分别在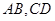 上,且
上,且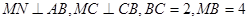 ,现将梯形
,现将梯形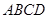 A沿
A沿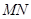 折起,使平面
折起,使平面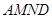 与平面
与平面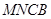 垂直(如图②).
垂直(如图②).(1)求证:
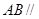 平面
平面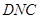 ;
;(2)当
 时,求二面角
时,求二面角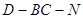 的大小.
的大小.
(1)证明:见解析;(2)∠NHD=30°。
(I)本小题属于翻折问题,本小题可以证明平面AMB//平面DNC即可.
(II)解本小题的关键是作出二面角的平面角,具体做法:过N作NH⊥BC交BC延长线于H,∵平面AMND⊥平面MNCB,DN⊥MN,∴DN⊥平面MBCN,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.
(1)证明:MB∥NC,MB?平面DNC,NC?平面DNC,
∴MB∥平面DNC………………………2
同理MA∥平面DNC,………………….3
又MA∩MB=M,且MA、MB?平面MAB.
 …………………..5
…………………..5
⇒AB∥平面DNC…………………………………7
(2)过N作NH⊥BC交BC延长线于H,……………………….8
∵平面AMND⊥平面MNCB,DN⊥MN,
∴DN⊥平面MBCN,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.………………….11
由MB=4,BC=2,∠MCB=90°知∠MBC=60°,
CN=4-2cos60°=3,∴NH=3sin60°= ………………….13
………………….13
由条件知:tanNHD=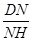 =
=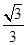 ,∴∠NHD=30°…………………..14
,∴∠NHD=30°…………………..14
(II)解本小题的关键是作出二面角的平面角,具体做法:过N作NH⊥BC交BC延长线于H,∵平面AMND⊥平面MNCB,DN⊥MN,∴DN⊥平面MBCN,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.
(1)证明:MB∥NC,MB?平面DNC,NC?平面DNC,
∴MB∥平面DNC………………………2
同理MA∥平面DNC,………………….3
又MA∩MB=M,且MA、MB?平面MAB.
 …………………..5
…………………..5⇒AB∥平面DNC…………………………………7
(2)过N作NH⊥BC交BC延长线于H,……………………….8
∵平面AMND⊥平面MNCB,DN⊥MN,
∴DN⊥平面MBCN,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.………………….11
由MB=4,BC=2,∠MCB=90°知∠MBC=60°,
CN=4-2cos60°=3,∴NH=3sin60°=
 ………………….13
………………….13由条件知:tanNHD=
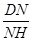 =
=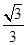 ,∴∠NHD=30°…………………..14
,∴∠NHD=30°…………………..14
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
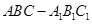 的侧棱与底面垂直,
的侧棱与底面垂直,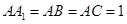 ,
,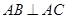 ,
,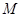 ,
,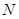 分别是
分别是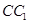 ,
,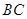 的中点,点
的中点,点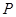 在直线
在直线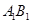 上,且
上,且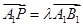 ;
;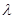 取何值,总有
取何值,总有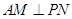 ;
;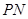 与平面
与平面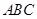 所成的角
所成的角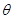 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;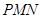 与平面
与平面
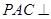 平面
平面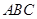 ,
,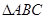 是以
是以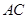 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,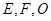 分别为
分别为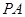 ,
,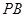 ,
,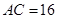 ,
,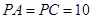 .
.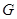 是
是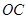 的中点,证明:
的中点,证明: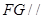 平面
平面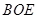 ;
;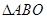 内是否存在一点
内是否存在一点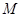 ,使
,使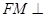 平面
平面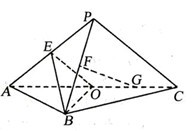
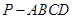 中,
中, 底面
底面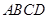 ,四边形
,四边形 ,
, ,
, ,
,
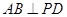 ;
;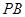 上找出一点
上找出一点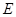 ,使
,使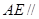 平面
平面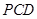 ,
,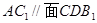 ;
;
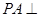 平面
平面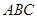 ,
,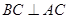 ,则图中直角三角形的个数为________.
,则图中直角三角形的个数为________.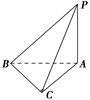
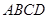 中,
中,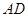 ⊥面
⊥面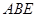 ,
,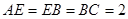 ,
,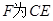 上的点,且
上的点,且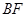 ⊥面
⊥面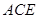 ,
,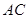 、
、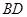 交于点
交于点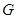 .
.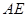 ⊥
⊥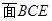 ;
;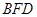 .
.
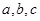 是三条直线,若
是三条直线,若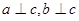 ,则
,则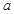 ∥
∥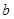 ”,得出如下结论:
”,得出如下结论: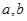 是两条直线,
是两条直线,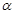 是平面,若
是平面,若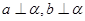 ,则
,则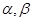 是两个平面,
是两个平面,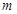 是直线,若
是直线,若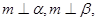 则
则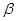 ;
;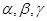 是三个平面,若
是三个平面,若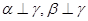 ,则
,则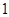
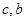 是两条直线,
是两条直线,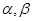 是两个平面,下列能推出
是两个平面,下列能推出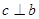 的是( )
的是( )