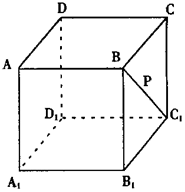
题目内容
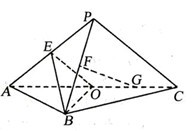
(本小题满分12分)如图,平面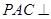 平面
平面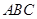 ,
,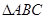 是以
是以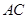 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,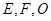 分别为
分别为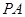 ,
,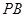 ,
,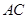 的中点,
的中点,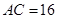 ,
,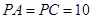 .
.
(1)设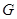 是
是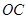 的中点,证明:
的中点,证明: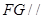 平面
平面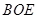 ;
;
(2)在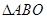 内是否存在一点
内是否存在一点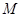 ,使
,使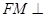 平面
平面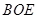 ,若存在,请找出点M,并求FM的长;若不存在,请说明理由。
,若存在,请找出点M,并求FM的长;若不存在,请说明理由。
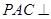 平面
平面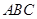 ,
,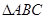 是以
是以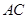 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,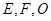 分别为
分别为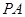 ,
,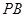 ,
,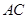 的中点,
的中点,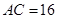 ,
,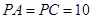 .
.(1)设
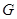 是
是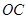 的中点,证明:
的中点,证明: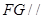 平面
平面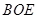 ;
;(2)在
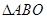 内是否存在一点
内是否存在一点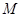 ,使
,使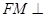 平面
平面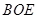 ,若存在,请找出点M,并求FM的长;若不存在,请说明理由。
,若存在,请找出点M,并求FM的长;若不存在,请说明理由。
证明:(1)见解析;(2) 。
。
 。
。本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,其中建立适当的坐标系,将线面平行及线面垂直问题,转化为向量夹角问题是解答本题的关键.本题综合较强,难度较大.
(I)连接OP,以O为坐标原点,分别以OB、OC、OP所在直线为x轴,y轴,z轴,建立空间直角坐标系O-xyz,分别求了各点对应的坐标,求出直线FG的方向向量和平面BOE的法向量,判断两个向量的关系,即可得到FG∥平面BOE;
(II)设点M的坐标为(x0,y0,0),则我们易求出直线FM的方向向量,由FM⊥平面BOE求出满足条件的M点的坐标,并与△ABO内部表示的平面区域对应的约束条件进行比照,即可得到答案.
证明:(1)取PE中点H,连结FH,GH,
∵ F,G分别为PB,OC中点,∴FH//BE,GH//EO,
∵ ,
, ,
,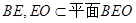 ,
,
∴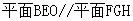 ,∵
,∵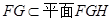 ,∴
,∴ 。 …………5分
。 …………5分
(2)∵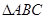 是以
是以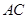 为斜边的等腰直角三角形,且O为AC中点,∴
为斜边的等腰直角三角形,且O为AC中点,∴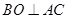 ,
,
又∵平面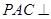 平面
平面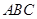 ,
,  ,
, ,
,
∴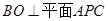 。
。
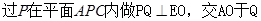 ,所以
,所以 ,
,
∵ ,∴
,∴ ,
,
 ,连结FM,因为点F为PB中点,
,连结FM,因为点F为PB中点,
则 ,进而
,进而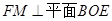 ,
, 。
。
 …………12分
…………12分
(I)连接OP,以O为坐标原点,分别以OB、OC、OP所在直线为x轴,y轴,z轴,建立空间直角坐标系O-xyz,分别求了各点对应的坐标,求出直线FG的方向向量和平面BOE的法向量,判断两个向量的关系,即可得到FG∥平面BOE;
(II)设点M的坐标为(x0,y0,0),则我们易求出直线FM的方向向量,由FM⊥平面BOE求出满足条件的M点的坐标,并与△ABO内部表示的平面区域对应的约束条件进行比照,即可得到答案.
证明:(1)取PE中点H,连结FH,GH,
∵ F,G分别为PB,OC中点,∴FH//BE,GH//EO,
∵
 ,
, ,
,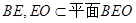 ,
,
∴
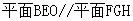 ,∵
,∵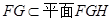 ,∴
,∴ 。 …………5分
。 …………5分(2)∵
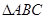 是以
是以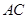 为斜边的等腰直角三角形,且O为AC中点,∴
为斜边的等腰直角三角形,且O为AC中点,∴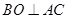 ,
,又∵平面
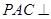 平面
平面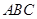 ,
,  ,
, ,
,∴
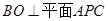 。
。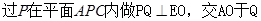 ,所以
,所以 ,
,∵
 ,∴
,∴ ,
, ,连结FM,因为点F为PB中点,
,连结FM,因为点F为PB中点,则
 ,进而
,进而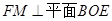 ,
, 。
。 …………12分
…………12分
练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
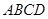 和矩形
和矩形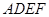 所在平面相互垂直,
所在平面相互垂直,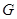 是
是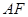 的中点.
的中点. 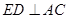 ;
;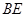 与平面
与平面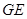 与
与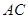 所成角的余弦值.
所成角的余弦值.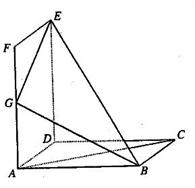
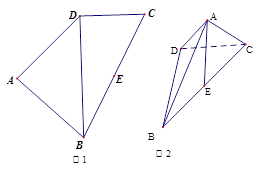
 中(图1),
中(图1),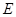 是
是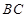 的中点,
的中点,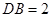 ,
,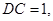
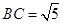 ,
,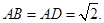 将(图1)沿直线
将(图1)沿直线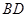 折起,使二面角
折起,使二面角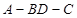 为
为 (如图2)
(如图2) 平面
平面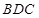 ;
;
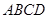 中,
中,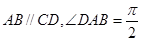 ,点
,点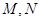 分别在
分别在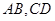 上,且
上,且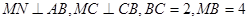 ,现将梯形
,现将梯形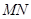 折起,使平面
折起,使平面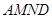 与平面
与平面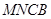 垂直(如图②).
垂直(如图②).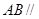 平面
平面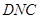 ;
; 时,求二面角
时,求二面角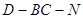 的大小.
的大小.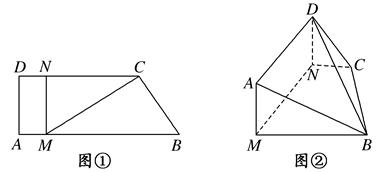
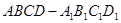 ,
, 是底
是底 对角线的交点.
对角线的交点.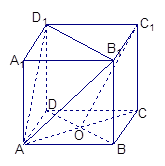
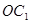 ∥面
∥面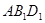 ;(2)
;(2)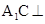 面
面 、
、 互相平行,则直线
互相平行,则直线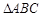 是正三角形,
是正三角形,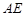 和
和 都垂直于平面
都垂直于平面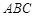 ,且
,且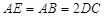 ,
,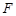 是
是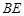 的中点.
的中点.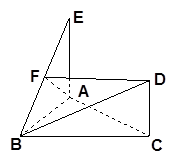
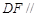 平面
平面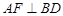 .
. 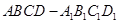 的面对角线
的面对角线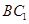 上运动,则下列四个命题:①三棱锥
上运动,则下列四个命题:①三棱锥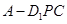 的体积不变; ②
的体积不变; ②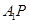 ∥面
∥面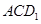 ; ③
; ③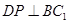 ; ④面
; ④面 面
面