题目内容
如图,在正三棱柱ABC—A1B1C1中,底面边长及侧棱长均为2,D是棱AB的中点,
(1)求证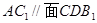 ;
;
(2)求异面直线AC1与B1C所成角的余弦值.

(1)求证
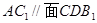 ;
;(2)求异面直线AC1与B1C所成角的余弦值.

(1)略;(2)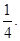
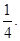
(1)连接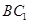 与
与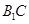 ,交点为
,交点为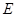 ,则
,则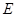 是
是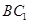 的中点,又D是棱AB的中点,所以
的中点,又D是棱AB的中点,所以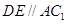 ,根据线面平行的判定定理可证出
,根据线面平行的判定定理可证出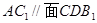 ;
;
(2)由(1)得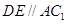 ,所以异面直线AC1与B1C所成的角就是
,所以异面直线AC1与B1C所成的角就是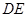 与
与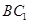 所成的角或其补角,在
所成的角或其补角,在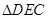 中,
中,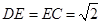 ,
, ,根据余弦定理求出异面直线AC1与B1C所成角的余弦值.
,根据余弦定理求出异面直线AC1与B1C所成角的余弦值.
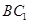 与
与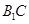 ,交点为
,交点为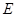 ,则
,则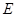 是
是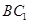 的中点,又D是棱AB的中点,所以
的中点,又D是棱AB的中点,所以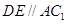 ,根据线面平行的判定定理可证出
,根据线面平行的判定定理可证出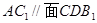 ;
;(2)由(1)得
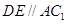 ,所以异面直线AC1与B1C所成的角就是
,所以异面直线AC1与B1C所成的角就是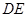 与
与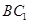 所成的角或其补角,在
所成的角或其补角,在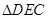 中,
中,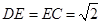 ,
, ,根据余弦定理求出异面直线AC1与B1C所成角的余弦值.
,根据余弦定理求出异面直线AC1与B1C所成角的余弦值.
练习册系列答案
相关题目
 中,AD∥BC,
中,AD∥BC, 平面
平面 ,
,  ,BC=6.
,BC=6.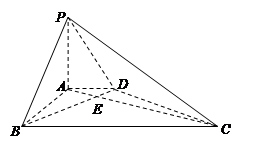
 的余弦值.
的余弦值. 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面 ,且
,且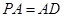 ,点
,点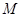 、
、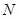 分别为侧棱
分别为侧棱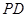 、
、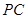 的中点
的中点 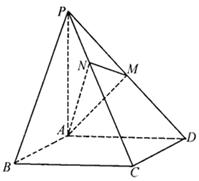
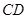 ∥平面
∥平面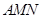 ;
;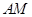 ⊥平面
⊥平面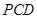 .
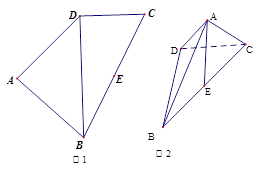
. 中(图1),
中(图1),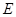 是
是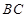 的中点,
的中点,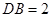 ,
,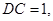
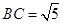 ,
,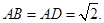 将(图1)沿直线
将(图1)沿直线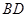 折起,使二面角
折起,使二面角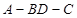 为
为 (如图2)
(如图2) 平面
平面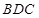 ;
;
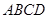 中,
中,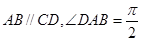 ,点
,点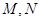 分别在
分别在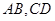 上,且
上,且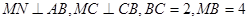 ,现将梯形
,现将梯形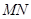 折起,使平面
折起,使平面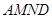 与平面
与平面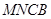 垂直(如图②).
垂直(如图②).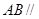 平面
平面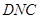 ;
; 时,求二面角
时,求二面角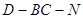 的大小.
的大小.
 中
中
 与
与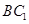 所成角的大小.
所成角的大小. 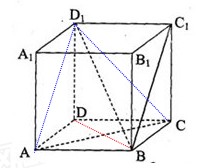
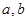 是两条直线,
是两条直线,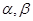 是两个平面,则下列4组条件中:①
是两个平面,则下列4组条件中:①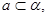
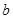 ∥
∥ ,
,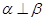 ;②
;②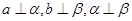 ;③
;③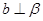 ,
,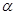 ∥
∥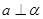 ,
,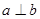 的条件有( )组。
的条件有( )组。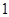
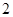
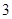
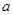 ,
,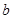 ,
,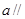 平面
平面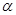 ,则
,则 平面
平面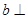 平面
平面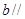 平面
平面