题目内容
已知x、y∈R+,且4x+y=1,求
+
的最小值.某同学做如下解答:
因为x、y∈R+,所以1=4x+y≥2
…①,
+
≥2
…②,
①×②得
+
≥2
•2
=24,所以
+
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时x、y的值______.
| 1 |
| x |
| 9 |
| y |
因为x、y∈R+,所以1=4x+y≥2
| 4xy |
| 1 |
| x |
| 9 |
| y |
|
①×②得
| 1 |
| x |
| 9 |
| y |
| 4xy |
|
| 1 |
| x |
| 9 |
| y |
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时x、y的值______.
其解答不正确.
因为x、y∈R+,所以1=4x+y≥2
…①,
+
≥2
…②,
①×②得
+
≥2
•2
=24,所以
+
的最小值为24.
其问题在:①等号成立的充要条件是4x=y=
;②等号成立的充要条件是y=9x,因此两个等号成立的条件不一样,即不能同时成立,故其最小值不是24.
其正确解答如下:∵x、y∈R+,且4x+y=1,
∴
+
=(4x+y)(
+
)=13+
+
≥13+2
=25,当且仅当y=6x=
时取等号.
因此
+
的最小值为25.
故答案为:25.
因为x、y∈R+,所以1=4x+y≥2
| 4xy |
| 1 |
| x |
| 9 |
| y |
|
①×②得
| 1 |
| x |
| 9 |
| y |
| 4xy |
|
| 1 |
| x |
| 9 |
| y |
其问题在:①等号成立的充要条件是4x=y=
| 1 |
| 2 |
其正确解答如下:∵x、y∈R+,且4x+y=1,
∴
| 1 |
| x |
| 9 |
| y |
| 1 |
| x |
| 9 |
| y |
| y |
| x |
| 36x |
| y |
|
| 3 |
| 5 |
因此
| 1 |
| x |
| 9 |
| y |
故答案为:25.

练习册系列答案
相关题目

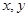 满足约束条件
满足约束条件 ,则
,则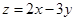 的最小值是( )
的最小值是( )



 ,
, 满足约束条件
满足约束条件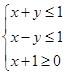 ,则
,则 的最小值为( )
的最小值为( )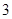



 满足约束条件
满足约束条件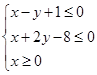 则
则 的最小值为________
的最小值为________