题目内容
已知两条直线l1:y=m和l2:y=
(m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时,
的最小值为( )
| 8 |
| 2m+1 |
| b |
| a |
A.16
| B.8
| C.8
| D.4
|
设A,B,C,D各点的横坐标分别为xA,xB,xC,xD,
则-log2xA=m,log2xB=m;-log2xC=
,log2xD=
;
∴xA=2-m,xB=2m,xC=2-
,xD=2
.
∴a=|xA-xC|,b=|xB-xD|,
∴
=
=|
|=2m•2
=2m+
.
又m>0,∴m+
=
(2m+1)+
-
≥2
-
=
(当且仅当m=
时取“=”)
∴
≥2
=8
.
故选B.
则-log2xA=m,log2xB=m;-log2xC=
| 8 |
| 2m+1 |
| 8 |
| 2m+1 |
∴xA=2-m,xB=2m,xC=2-
| 8 |
| 2m+1 |
| 8 |
| 2m+1 |
∴a=|xA-xC|,b=|xB-xD|,
∴
| b |
| a |
| |xB-xD| |
| |xA-xC| |
2m-2
| ||
2-m-2-
|
| 8 |
| 2m+1 |
| 8 |
| 2m+1 |
又m>0,∴m+
| 8 |
| 2m+1 |
| 1 |
| 2 |
| 8 |
| 2m+1 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
∴
| b |
| a |
| 7 |
| 2 |
| 2 |
故选B.

练习册系列答案
相关题目

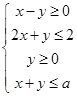 ,表示的平面区域是一个三角形区域,则
,表示的平面区域是一个三角形区域,则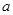 的取值范围是( )
的取值范围是( )

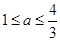
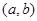 在直线
在直线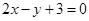 的右下方,则( )
的右下方,则( )