题目内容

如图所示，有一边长分别为8与5的长方形，在各角剪去相同的小正方形，把四边折起作成一个无盖小盒，要使纸盒的容积最大，求剪去的小正方形的边长及容积最大值．
设剪去的小正方形的边长为a，
则纸盒的容积为V=a（8-2a）（5-2a），（0＜a＜
5
2
）
∴V=4a3-26a2+40a，
∴V′=12a2-52a+40=4（a-1）（3a-10）
∴0＜a＜1，V′＞0；
1＜a＜
5
2
，V′＜0，
∴函数在（0，1）上单调递增，在（1，
5
2
）上单调递减，
∴a=1时，函数取得极大值，且为最大值，
∴剪去的小正方形的边长为1，容积最大值为18．
练习册系列答案
相关题目
设x，y为正实数且满足
4
x
+
9
y
=1，则xy有（　　）
A．最小值12B．最大值12C．最小值144D．最大值144
设函数f(x)=
ax2+1
bx
(a，b∈Z+)满足f（1）=2，f（2）＜3．
（1）求a，b的值；
（2）当x≥
1
2
时，求出f（x）的值域．
某个集团公司下属的甲、乙两个企业在2012年1月的产值都为a万元，甲企业每个月的产值与前一个月相比增加的产值相等，乙企业每个月的产值与前一个月相比增加的百分数相等，到2013年1月两个企业的产值再次相等．
（1）试比较2012年7月甲、乙两个企业产值的大小，并说明理由；
（2）甲企业为了提高产能，决定投入3.2万元买台仪器，并且从2013年2月1日起投入使用．从启用的第一天起连续使用，第n天的维修保养费为
n+49
10
元（n∈N*），求前n天这台仪器的日平均耗费（含仪器的购置费），并求日平均耗资最小时使用的天数？
下列四个结论中，正确结论为（　　）
A．当x＞0且x≠1时，lgx+
1
lgx
≥2
B．当x＞0时，
x
+
1
x
≥2
C．当x≥0时，x+
1
x
的最小值为2
D．当x＞0时，x3+
1
x
的最小值为2
某企业有两个生产车间分别在A、B两个位置，A车间有100名员工，B车间有400名员工，现要在公路AC上找一点D，修一条公路BD，并在D处建一个食堂，使得所有员工均在此食堂用餐，已知A、B、C中任意两点间的距离均是1km，设∠BDC=α，所有员工从车间到食堂步行的总路程为S．
（1）写出S关于α的函数表达式，并指出α的取值范围；
（2）问食堂D建在距离A多远时，可使总路程S最少？
已知x、y∈R+，且4x+y=1，求
1
x
+
9
y
的最小值．某同学做如下解答：
因为x、y∈R+，所以1=4x+y≥2
4xy
…①，
1
x
+
9
y
≥2
9
xy
…②，
①×②得
1
x
+
9
y
≥2
4xy
•2
9
xy
=24，所以
1
x
+
9
y
的最小值为24．
判断该同学解答是否正确，若不正确，请在以下空格内填写正确的最小值；若正确，请在以下空格内填写取得最小值时x、y的值______．
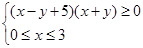不等式组表示的平面区域是一个（  ）.
A．三角形B．直角三角形C．梯形D．矩形
已知a＞b＞0，则下列不等式中总成立的是（　　）
A．a+
1
b
＞b+
1
a
B．a+
1
a
＞b+
1
b
C．
b
a
＞
b+1
a+1
D．b-
1
b
＞a-
1
a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网