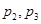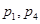题目内容
已知正实数a,b满足a+2b=1,则a2+4b2+
的最小值为( )
| 1 |
| ab |
A.
| B.4 | C.
| D.
|
∵已知正实数a,b满足a+2b=1,∴1=a+2b≥2
,当且仅当a=2b时,取等号.解得ab≤
,即ab∈(0,
].
再由 (a+2b)2=a2+4b2+4ab=1,故 a2+4b2+
=1-4ab+
.
把ab当做自变量,则1-4ab+
在(0,
]上是减函数,故当ab=
时,1-4ab+
取得最小值为 1-
+8=
,
故选D.
| 2ab |
| 1 |
| 8 |
| 1 |
| 8 |
再由 (a+2b)2=a2+4b2+4ab=1,故 a2+4b2+
| 1 |
| ab |
| 1 |
| ab |
把ab当做自变量,则1-4ab+
| 1 |
| ab |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| ab |
| 1 |
| 2 |
| 17 |
| 2 |
故选D.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

 内的一个动点,则
内的一个动点,则 的最小值为( ).
的最小值为( ).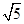


 与连接
与连接 ,
, 的线段相交,则
的线段相交,则 的取值范围是( )
的取值范围是( )



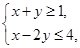 的解集为D,有下面四个命题:
的解集为D,有下面四个命题: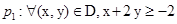 ,
, 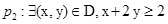 ,
,
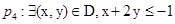 ,
,